[알고리즘] 크루스칼(Kruskal)과 프림(Prim)

Goal

MST란?
크루스칼이란?
프림이란?

최소 신장 트리에 사용된 최소 비용을 어떻게 구할까?

최소 비용으로 신장 트리를 어떻게 만들 수 있을까?

1. 크루스칼? 프림? MST?

1) MST(Minimum Spanning Tree)

신장 트리(Spanning Tree)

무방향 그래프 G(V,E)에서 E에 속한 간선들로 사이클을 포함하지 않으면서 모든 정점 V를 연결한 부분 그래프를 신장 트리(Spanning Tree)라 한다.

그래프에서 신장 트리는 여러 형태로 존재할 수 있으며, 신장 트리의 특징은 n개의 정점을 갖는 그래프에서 신장 트리에 속하는 간선의 수는 n-1개이며 사이클을 이루지 않는다는 특징이 있다.

MST란 최소 비용 신장 트리(이하 최소 신장 트리)를 뜻하며, 무방향 그래프의 간선들에 가중치가 주어진 경우, 여러 신장 트리 중에 간선들의 가중치 합이 최소인 신장 트리를 말한다.

효율적인 통신 망 설계 등에 이용될 수 있다.

2) 크루스칼(Kruskal)

크루스칼이란 위에서 말한 최소 신장 트리를 구하는 알고리즘이다.

크루스칼은 greedy하게(결정의 순간마다 최선의 결정을 함으로써 최종적인 해답에 도달) 모든 정점을 최소 비용으로 연결하여 최소 신장 트리를 구한다.

크루스칼의 핵심은 모든 간선을 가중치 기준으로 오름차순으로 정렬하고,

이 간선들을 순서대로 모든 정점이 연결될 때까지 연결하는 것이다.

Union-Find 알고리즘을 이용해서 구현할 수 있고, 이를 통해 사이클이 형성되지 않으면서 모든 정점을 연결할 수 있다.

Union-Find 알고리즘은 O(1) 즉 상수 시간 복잡도를 가지기 때문에

간선을 정렬하는 로직이 전체 시간 복잡도를 좌우하게 되는데,

가장 일반적인 퀵 정렬을 예로 들면, 퀵 정렬의 시간 복잡도인 O(ElogE)가 크루스칼 알고리즘의 시간 복잡도가 된다.

//E : 간선의 개수

//V : 정점의 개수

크루스칼 알고리즘의 동작 방식

1. 그래프의 간선들을 가중치 기준 오름차순으로 정렬한다.

2-1. 정렬된 간선 리스트를 순서대로 선택하여, 간선의 정점들을 연결한다.

2-2. 이때 정점을 연결하는 것은 Union-Find의 Union으로 구현한다.

3. 만약 간선의 두 정점 a,b가 이미 연결되어 있다면 스킵한다.

4. 위의 과정을 반복하여 최소 비용의 간선들만 이용하여 모든 정점이 연결된다.

아래에서 직접 로직을 따라가 보고, 직접 코드로 구현해보자.

3) 프림(Prim)

프림도 위에서 말한 최소 신장 트리를 구하는 알고리즘이다.

프림은 임의의 시작점에서 현재까지 연결된 정점들에서 연결되지 않은 정점들에 대해, 가장 가중치가 작은 정점을 연결하는 정점 선택 기반으로 동작한다.

프림의 핵심은 트리 집합을 단계적으로 확장하는 것이고,

새로운 정점을 연결할 때마다 새로운 정점에서 갈 수 있는 아직 연결되지 않은 정점들에 대한 간선을 추가해줘야 한다.

Priority Queue를 이용한 최소 힙으로 구현할 수 있고, 다익스트라 알고리즘과 구현 방식이 유사하다.

최소 힙으로 구현한 프림의 시간 복잡도를 구해보자.

시작점부터, 모든 정점을 탐색하는데 이 정점들은 최소 힙의 extract-min 값들이다.

따라서 모든 정점 V * extract-min에 소요되는 logV 즉 O(VlogV)이고,

정점들에서 갈 수 있는 정점들을 연결하는 간선들을 최소 힙에 추가하는 것은 최대 E번이며,

최소 힙에 최대 V개의 정점이 들어오기 때문에,

추가된 정점의 가중치를 최소 힙 내부에서 정렬하는 것은 decrease-key로 최대 logV만큼 수행된다.

따라서 모든 간선 E * 간선을 통해 삽입된 정점의 가중치 정렬 logV 즉 O(ElogV)이다.

따라서 전체 로직에 걸리는 시간은 VlogV + ElogV라고 할 수 있는데,

간선의 수는 정점의 수보다 많기 때문에 시간 복잡도에선 VlogV를 무시하여

O(ElogV)가 프림 알고리즘의 시간 복잡도가 된다.

최소 힙을 사용하지 않는 경우 O(V^2)의 시간 복잡도를 가질 수 있지만,

최소 힙으로 구현하는 것이 어렵지 않다.

또한, 피보나치 힙을 이용하는 경우 O(E + VlogV)의 시간 복잡도가 가능하지만,

대부분의 경우 최소 힙이면 충분하니 여기까지만 알아보자.

//E : 간선의 개수

//V : 정점의 개수

프림 알고리즘의 동작 방식

1. 임의의 정점을 시작점으로 선택한다.

2. 시작점에서 갈 수 있는 정점 중 가장 가중치가 작은 정점을 연결한다.

3-1. 2번 과정에서 시작점과 어떠한 정점들이 연결되었다.

3-2. 시작점과 연결된 정점들을 a집합이라 할 때, a집합에서 갈 수 있는 a집합에 속하지 않은 정점들에 대해 가중치가
가장 작은 정점을 연결한다.

4. a집합의 크기가 늘어났다.(시작점을 포함한 a집합에 새로운 정점을 연결했다.) 위의 과정을 모든 정점이 연결될
때까지 반복한다.

2. 크루스칼(Kruskal) 동작 방식

위와 같은 그래프에서 크루스칼 알고리즘의 동작 방식으로 MST(최소 신장 트리)를 구해보자.

크루스칼 알고리즘은, 간선을 가중치 기준 오름차순으로 정렬한 후, 순서대로 연결한다고 했다.

위의 그래프에서 가장 가중치가 적은 간선은 B-D 간선이다.

1.

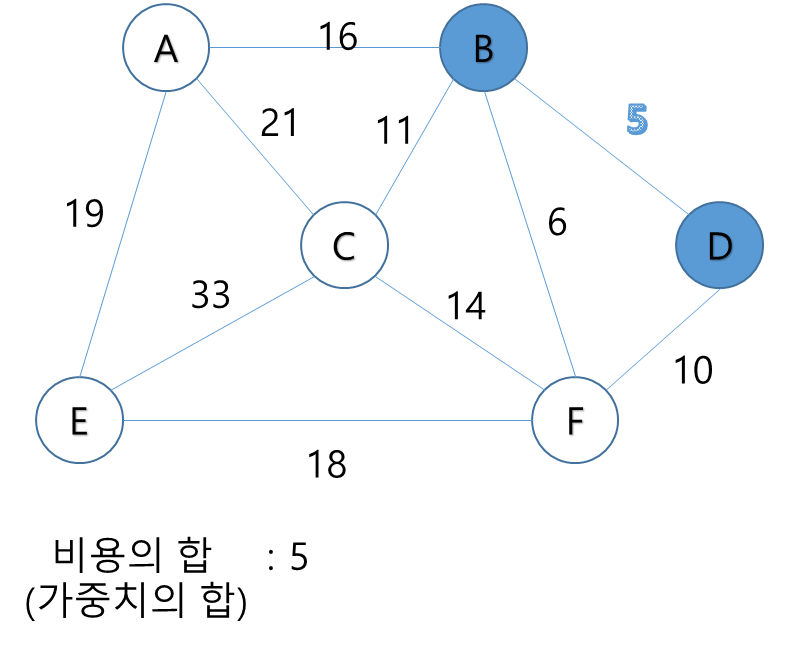
주어진 그래프의 간선 중 가장 가중치가 적은 간선 B-D를 연결한다.

2.

그다음, 가중치가 가장 적은 간선 B-F를 연결한다.

3.

그다음, 가중치가 가장 적은 간선은 D-F이지만, D와 F는 B를 통해 이미 연결되어 있다. 따라서 D-F는 굳이 연결할 필요가 없기 때문에, 그 다음 가중치가 가장 적은 간선인 B-C를 연결한다.

4.

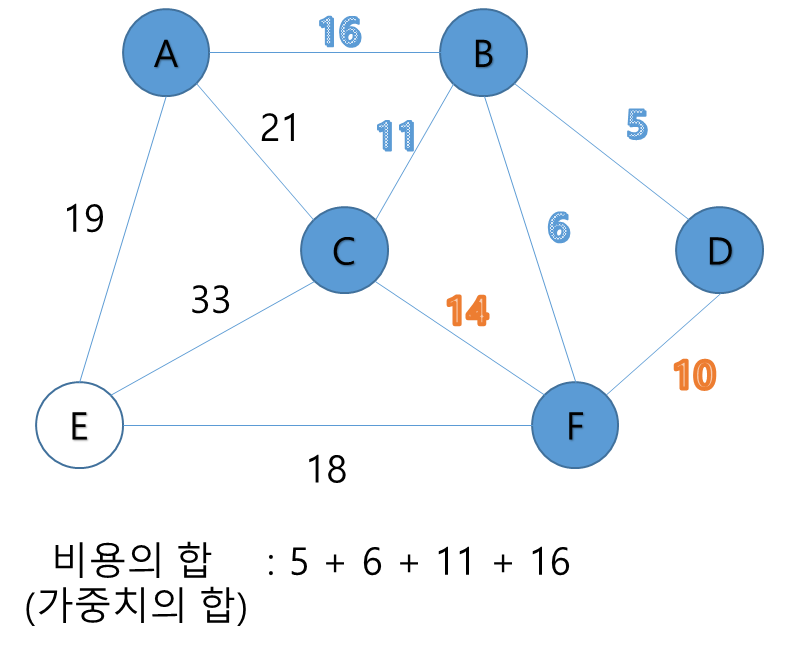
마찬가지로, 그다음 가중치가 가장 적은 간선은 C-F 간선이지만, C와F 정점도 이미 연결되어 있기 때문에 스킵하고,

그다음 가중치가 적은 간선인 A-B를 연결한다.

5.

모든 정점이 연결되었고, 정점을 연결할 때마다 가중치가 가장 적은 간선을 선택해왔기 때문에, 모든 정점이 연결된 순간 사용된 간선들의 가중치의 합은 최솟값임을 보장한다!

이때 비용의 합은 56이고, 사용된 간선은 5(n-1)개이다.

3. 프림(Prim) 동작 방식

같은 그래프에서 프림 알고리즘의 동작 방식으로 MST(최소 신장 트리)를 구해보자.

프림 알고리즘은 임의의 정점을 시작점으로 잡고, 트리에 아직 연결되지 않은 정점들에 대해 최소 가중치를 갖는 정점을 연결해나가며 트리를 단계적으로 확장한다고 했다.

위의 그래프에서 정점 E를 시작점으로 최소 신장 트리를 구해보자.

1.

시작점 E에서 갈 수 있는 정점 중(인접한 정점) 가중치가 가장 작은 간선으로 연결된 정점인 F를 연결한다.

2.

E와 F로 연결된 집합(빨간색 원)에서 갈 수 있는 정점 중 가중치가 가장 작은 간선으로 연결된 정점인 B를 연결한다.

3.

E, F, B로 연결된 집합에서 갈 수 있는 정점 중 가중치가 가장 작은 간선으로 연결된 정점인 D를 연결한다.

4.

E,F,B,D로 연결된 집합에서 갈 수 있는 정점 중 가중치가 가장 작은 간선으로 연결된 정점인 C를 연결한다.

5.

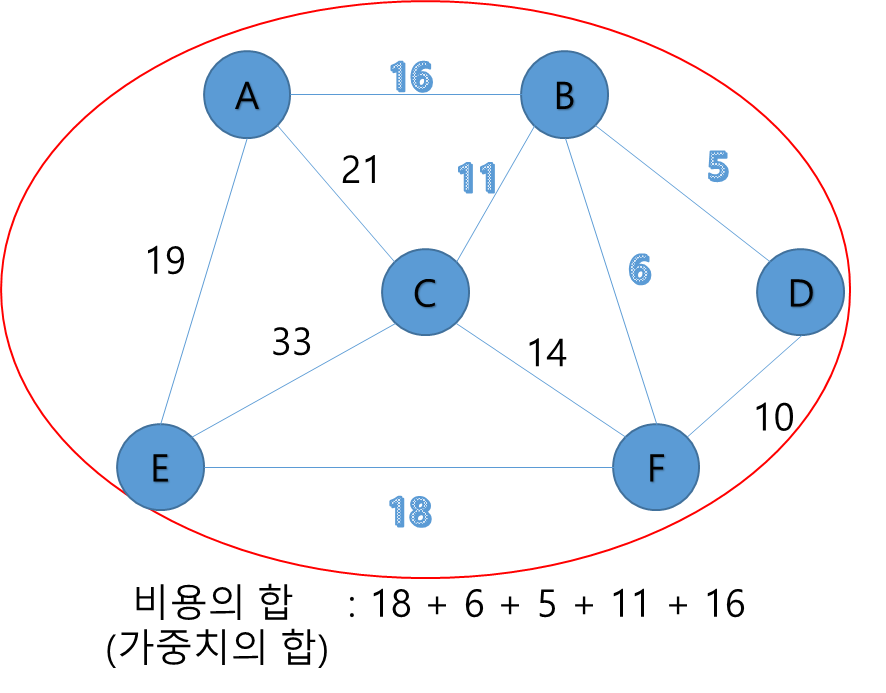
E,F,B,D,C로 연결된 집합에서 갈 수 있는 정점 중 가중치가 가장 작은 간선으로 연결된 정점 A를 연결한다.

모든 정점이 연결되었으므로 최소 신장 트리가 완성되었다.

트리를 확장해 나가면서 트리에서 연결할 수 있는 정점 중 가장 가중치가 작은 간선만을 사용했기 때문에 이 또한 가중치의 합이 최소임을 보장한다.

이때 비용의 합은 56이고, 사용된 간선은 5(n-1)개 이다.

4. 크루스칼(Kruskal) 구현

코드(C++)

#include<iostream>
#include<vector>
#include <algorithm>

using namespace std;

//각 정점마다 하나의 부모(parent) 정점으로 연결됨을 표시한다.
int parent[6];

//정점에 연결된 부모 정점을 반환
int getParent(int x) {
	if (parent[x] == x) return x;
	return parent[x] = getParent(parent[x]); // 연결되어있는 부모 정점을 반환하는 동시에, 연결되어있는 정점들의 부모 정점을 갱신 
}

//두 정점을 연결
void unionParent(int a, int b) {
	a = getParent(a);
	b = getParent(b);
	//a와 b중 부모 정점이 작은 쪽으로 합치기
	if (a < b) parent[b] = a;
	else parent[a] = b;
}

//두 정점이 연결되어있는지 확인
bool findParent(int a, int b) {
	a = getParent(a);
	b = getParent(b);
	if (a == b) return 1;
	else return 0;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	//가중치의 합
	int answer = 0;

	//각 정점의 부모 정점을 본인으로 초기값 설정
	for (int i = 0; i < 6; i++) {
		parent[i] = i;
	}

	//pair.first = 가중치
	//pair.second.first, pair.second.second = 간선으로 이어진 a,b 정점
	vector<pair<int, pair<int, int>>> edge;
	//간선 저장
	edge.push_back({ 16, {0, 1 } });
	edge.push_back({ 21, {0, 2 } });
	edge.push_back({ 19, {0, 4 } });
	edge.push_back({ 11, {1, 2 } });
	edge.push_back({ 5, {1, 3 } });
	edge.push_back({ 6, {1, 5 } });
	edge.push_back({ 33, {2, 4 } });
	edge.push_back({ 14, {2, 5 } });
	edge.push_back({ 10, {3, 5 } });
	edge.push_back({ 18, {4, 5 } });

	//간선을 가중치 기준 오름차순으로 정렬
	sort(edge.begin(), edge.end());

	cout << "사용된 간선\n";
	//모든 간선을 가중치가 낮은 순서대로 검사
	for (int i = 0; i < edge.size(); i++) {
		//간선의 두 정점이 연결되지 않았다면 두 정점을 연결
		if (!findParent(edge[i].second.first, edge[i].second.second)) {
			//가중치의 합에 사용된 간선의 가중치를 누적
			answer += edge[i].first;
			//간선의 두 정점을 연결
			unionParent(edge[i].second.first, edge[i].second.second);
			cout << "가중치 : " << edge[i].first << " 두 정점 : " << edge[i].second.first << ' ' << edge[i].second.second << '\n';
		}
	}
	cout <<"가중치의 합"<< answer;

	return 0;
}

5. 프림(Prim) 구현

코드(C++)

#include<iostream>
#include<vector>
#include <queue>

using namespace std;

//pair.first = 가중치
//정점 a,b로 이어진 간선
//edge의 인덱스 = a
//pair.second = b
vector<pair<int, int>> edge[6];

//연결된 정점인지 저장
bool visited[6];

//사용한 가중치들의 합 저장
int answer;
void prim() {
	
	//pq.first = 가중치
	//pq.second = 정점
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int,int>>> pq;
	//임의의 정점에서 시작
	pq.push({ 0,0 });
	
	cout << "사용된 간선\n";

	while (!pq.empty()) {
		
		//pq의 탑은 현재 연결된 정점들의 집합에서 갈 수 있는 정점 중 가장 가중치가 적은 정점
		//가장 가까운 정점을 저장 후 pop
		int curNode = pq.top().second;
		int curDis = pq.top().first;
		pq.pop();
		//이 정점이 이미 연결되어있다면 스킵
		if (visited[curNode]) continue;
		//이 정점이 연결되어있지 않다면 연결
		visited[curNode] = true;
		answer += curDis;
		
		cout << "연결된 정점들 : ";
		for (int i = 0; i < 6; i++) {
			if (visited[i])
				cout << i << ' ';
		}
		
		cout << "    사용한 가중치 : " << curDis << '\n';

		//새로 연결된 정점에서 갈 수 있는 정점들을 추가
		for (int i = 0; i< edge[curNode].size();i++) {
			int nextNode = edge[curNode][i].second;
			int nextDis = edge[curNode][i].first;

			//현재 정점에서 갈 수 있는 정점이 이미 연결되어있다면 추가하지 않고 스킵
			if (visited[nextNode]) continue;

			//아직 연결되지 않은 정점,가중치를 모두 pq에 삽입
			pq.push({ nextDis,nextNode });
			
		}

	}
	
	cout <<"가중치의 합 : "<< answer<<'\n';
}


int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	//양방향 간선 저장
	edge[0].push_back({ 16,1 });
	edge[1].push_back({ 16,0 });
	edge[0].push_back({ 21,2 });
	edge[2].push_back({ 21,0 });
	edge[0].push_back({ 19,4 });
	edge[4].push_back({ 19,0 });
	edge[1].push_back({ 11,2 });
	edge[2].push_back({ 11,1 });
	edge[1].push_back({ 5,3 });
	edge[3].push_back({ 5,1 });
	edge[1].push_back({ 6,5 });
	edge[5].push_back({ 6,1 });
	edge[2].push_back({ 33,4 });
	edge[4].push_back({ 33,2 });
	edge[2].push_back({ 14,5 });
	edge[5].push_back({ 14,2 });
	edge[3].push_back({ 10,5 });
	edge[5].push_back({ 10,3 });
	edge[4].push_back({ 18,5 });
	edge[5].push_back({ 18,4 });

	prim();
	
	return 0;
}

6. 크루스칼 vs 프림

두 알고리즘 모두 MST를 구하는 알고리즘이지만, 동작 방식이 다르기 때문에 상황에 따라 적절하게 사용해야 한다.

프림의 시간 복잡도는 O(ElogV)

크루스칼의 시간 복잡도는 O(ElogE)

즉, 그래프 내의 간선이 많은 경우는 프림 알고리즘,

간선이 적은 경우는 크루스칼 알고리즘이 유리하다.

2021.08.26 - [알고리즘 문제 풀이/프로그래머스] - 프로그래머스 섬 연결하기 c++, Kotlin (MST)

2021.09.01 - [알고리즘 문제 풀이/백준] - 백준 21924 도시 건설 Kotlin (MST)

2021.10.07 - [알고리즘 문제 풀이/백준] - 백준 1922 네트워크 연결 c++ (MST)

2021.10.07 - [알고리즘 문제 풀이/백준] - 백준 1647 도시 분할 계획 c++ (MST)

2021.12.13 - [알고리즘 문제 풀이/백준] - 백준 1939 중량제한 Kotlin (크루스칼, 프림, 이분 탐색)

2021.12.14 - [알고리즘 문제 풀이/백준] - 백준 16398 행성 연결 Kotlin (mst)

2021.12.14 - [알고리즘 문제 풀이/백준] - 백준 1774 우주신과의 교감 Kotlin (mst)

8. 마무리

구현 방식에는 사람마다 차이가 있기 때문에, 제 코드가 정답이 아닙니다.

더 좋은 방식이 있거나, 위의 개념 중에 오 개념이 있는 경우 댓글로 알려주시면 감사하겠습니다 :)

c++코드를 올렸는데, Kotlin 코드도 필요하시다면 말씀해주세요.

References

https://victorydntmd.tistory.com/102

http://egloos.zum.com/itfs/v/9772949

https://ko.wikipedia.org/wiki/%ED%94%84%EB%A6%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

저작자표시

'알고리즘' 카테고리의 다른 글

[알고리즘] Graph-위상 정렬(Topological Sort) (0)	2021.07.24
[알고리즘] 분할 정복(Divide and Conquer) (0)	2021.07.21
[알고리즘] 병합/합병 정렬(Merge Sort) (0)	2021.07.21
[알고리즘] 퀵 정렬(Quick Sort) (1)	2021.07.19
[알고리즘] 삽입 정렬 (Insertion Sort) (0)	2021.07.18

옹벨 일기

[알고리즘] 크루스칼(Kruskal)과 프림(Prim)

Goal

1. 크루스칼? 프림? MST?

1) MST(Minimum Spanning Tree)

2) 크루스칼(Kruskal)

3) 프림(Prim)

2. 크루스칼(Kruskal) 동작 방식

1.

2.

3.

4.

5.

3. 프림(Prim) 동작 방식

1.

2.

3.

4.

5.

4. 크루스칼(Kruskal) 구현

코드(C++)

5. 프림(Prim) 구현

코드(C++)

6. 크루스칼 vs 프림

7. 관련 문제

8. 마무리

'알고리즘' 카테고리의 다른 글

댓글

티스토리툴바

[알고리즘] 크루스칼(Kruskal)과 프림(Prim)

Goal

1. 크루스칼? 프림? MST?

1) MST(Minimum Spanning Tree)

2) 크루스칼(Kruskal)

3) 프림(Prim)

2. 크루스칼(Kruskal) 동작 방식

1.

2.

3.

4.

5.

3. 프림(Prim) 동작 방식

1.

2.

3.

4.

5.

4. 크루스칼(Kruskal) 구현

코드(C++)

5. 프림(Prim) 구현

코드(C++)

6. 크루스칼 vs 프림

7. 관련 문제

8. 마무리

'알고리즘' 카테고리의 다른 글

관련글

댓글

티스토리툴바