
병합 정렬(Merge Sort)이란?
리스트를 반으로 더 이상 나눌 수 없을 때까지 반으로 나누고(Divide : 분할),
나누어진 부분 리스트들을 두 개씩 짝지어 정렬(Conquer : 정복)하며 합치는(Combine : 결합) 과정을 반복하는 방법으로
원소들을 작은 순, 혹은 큰 순으로 정렬하는 알고리즘 중 하나이다.
병합 정렬(Merge Sort)의 특징
1. 주어진 배열(입력 배열) 이외에 다른 추가 메모리를 요구한다.
//추가적인 리스트가 필요하다.
2. 중복된 값은 입력 순서와 동일하게 정렬되는 안정 정렬(Stable Sort)이다.
// merge할 때 같은 값이 나온다면 앞의 그룹의 숫자를 먼저 써야 함
3. 데이터들 간의 상대적 크기 관계만을 이용해서 정렬하는 비교 정렬이다
4. 시간 복잡도는 Best, Avg, Worst의 경우 모두 O(NlogN)으로, 퀵 정렬(Quick Sort)에 반해 최악의 경우에도
O(NlogN)을 보장한다.
5. 분할 정복 알고리즘을 기반으로 정렬되는 방식으로, 퀵 정렬(Quick Sort)은 피벗 값에 따라 편향되게 분할할 가능성이 있으나, 병합 정렬(Merge Sort)의 경우 항상 반절씩 나누기 때문에, 리스트가 균등하게 나뉜다.
//분할 정복(divide and conquer)
//주어진 문제를 작은 사례로 나누고(Divide : 분할), 각각의 작은 문제들을 해결하여 합치는(Conquer : 정복) 방법이다.
//대개 재귀 호출을 이용하여 구현한다.
6. 일반적으로 퀵 정렬(Quick Sort)보다 느리다.
병합 정렬(Merge Sort) 결과
주어진 배열을 오름차순 혹은 내림차순으로 정렬
병합 정렬(Merge Sort) 구현 방법
1. 한 개의 리스트를 더 이상 나눠질 수 없을 때까지 반으로 냅다 쪼갠다.(Divide : 분할)
2. 더 이상 리스트를 나눌 수 없으면, 반절씩 반복적으로 나누어진 부분 리스트들을 정렬하며 합친다.
//합치는 순간에 정렬이 수행된다. (Conquer : 정복, Combine : 결합)
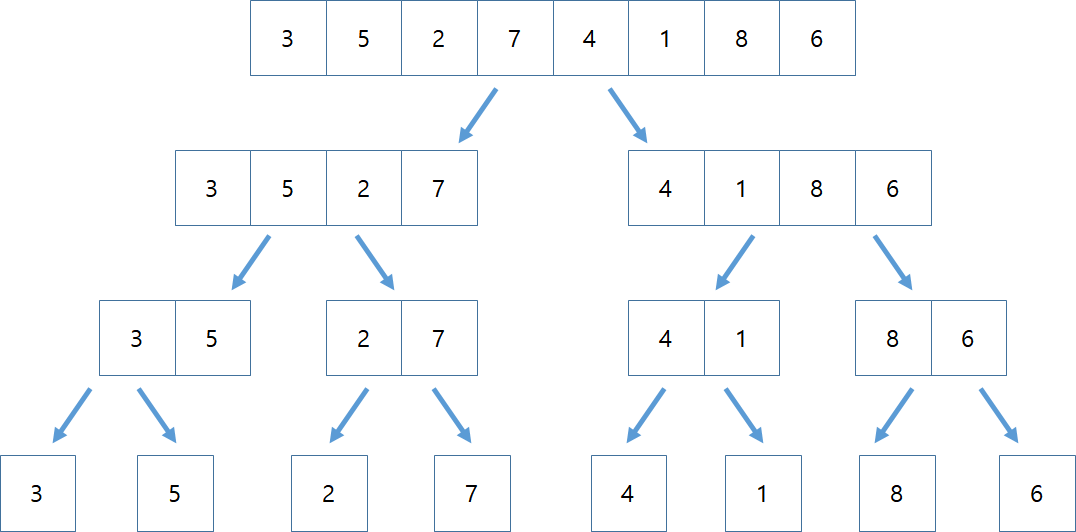
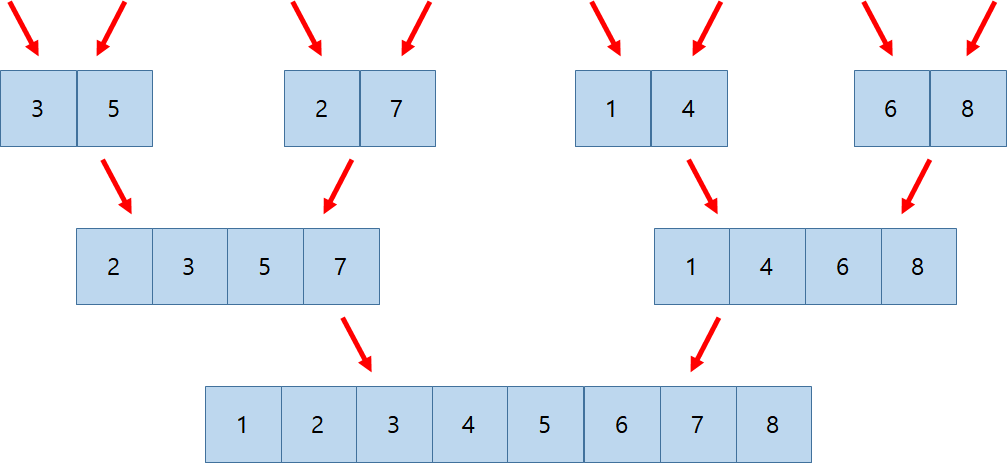
나의 직관적인 그림에 단박에 과정이 이해됐으리라.
이제 합치는 과정에서 어떻게 정렬이 이루어지는지 확인해보자.

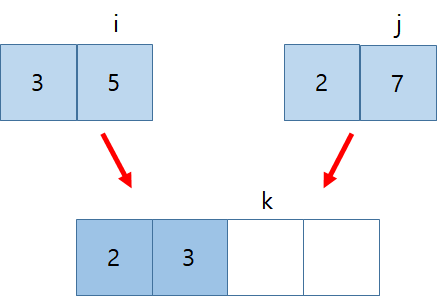
위의 두 개의 분할 리스트에서,
왼쪽 리스트의 첫 번째 인덱스를 i,
오른쪽 리스트의 첫 번째 인덱스를 j,
합쳐질 리스트의 첫 번째 인덱스를 k라고 하자.
i의 값과, j의 값을 비교했을 때, j의 값이 더 작기 때문에 다음과 같은 그림이 된다.

위와 같이, i의 값(3)과 j의 값(2)을 비교해서 작은 값을 합쳐질 리스트의 k번째 인덱스에 넣고,
k를 1증가, j를 1증가 시킨다.
i의 값(3)과 j의 값(7)을 비교했을 때, i의 값인 3이 더 작기 때문에
새로운 리스트의 k번째 인덱스에 i의 값(3)을 넣고 i와 k를 1씩 증가시킨다.

i의 값(5)와 j의 값(7)을 비교했을 때, i의 값인 5가 더 작기 때문에
새로운 리스트의 k번째 인덱스에 i의 값(5)을 넣고 i와 k를 1씩 증가시킨다.

i가 왼쪽 리스트의 인덱스를 벗어났기 때문에, 오른쪽 리스트의 남은 값들을 차례대로 합쳐질 리스트에 넣고
해당 분할-정복을 종료한다.
시간 복잡도가 항상 O(N^2)?

크기(N)가 8인 리스트를 모두 분할하는 데까지 총 3단계가 걸렸고,(log8=3)

크기가 2인 리스트 두 개를 크기가 4인 리스트로 정렬 및 결합하는 과정에서는 총 4번의 정렬 및 결합이 이루어졌다.
즉. 다시 크기가 8인 리스트로 정렬 및 결합하는 과정에서는 총 8(N)만큼 동작한다.
따라서, 분할하는 과정 logN, 정렬 및 결합하는 과정 N으로 O(NlogN)의 시간 복잡도를 보장하게 되는 것이다.
다만 일반적으로 퀵 정렬보다 느리며, 메모리 활용이 비효율적이라는 점에 유의하자.
코드(c++)
#include <iostream>
using namespace std;
//쪼개지는 부분 리스트들을 모두 생성할 필요 없이 정렬에 쓰일 하나의 리스트만 생성한다.
int sorted[8];
//
void merge(int arr[], int start, int end) {//정렬 및 결합 함수
int mid = (start + end) / 2;
int i = start;
int j = mid + 1;
int k = start;
//왼쪽 리스트와 오른쪽 리스트의 값을 비교(정렬)하면서 sorted란 배열에 합친다.
while (i <= mid && j <= end) {
if (arr[i] < arr[j]) {
sorted[k++] = arr[i++];
}
else {
sorted[k++] = arr[j++];
}
}
//남은 값 모두 넣기
if (i > mid) {
while (j <= end) {
sorted[k++] = arr[j++];
}
}
if(j>end){
while (i <= mid) {
sorted[k++] = arr[i++];
}
}
for (int i = 0; i <= end; i++) {
arr[i] = sorted[i];
cout << arr[i] << ' ';
}
cout << '\n';
}
//주어진 정렬을 더 이상 나눌 수 없을 때 까지 쪼갠 후, 크기가 1인 배열들을 순차적으로 합치며 정렬한다.
void mergeSort(int arr[],int start, int end) {//분할 함수
if (start < end) {
int mid = (start + end) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
merge(arr, start, end);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
//정렬할 배열
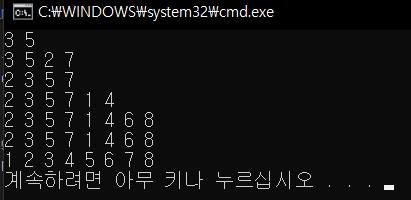
int arr[8] = { 3,5,2,7,4,1,8,6 };
//병합 정렬 실행
mergeSort(arr,0,7);
/*for (int i = 0; i < 8; i++) {
cout << arr[i] << ' ';
}*/
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] Graph-위상 정렬(Topological Sort) (0) | 2021.07.24 |
|---|---|
| [알고리즘] 분할 정복(Divide and Conquer) (0) | 2021.07.21 |
| [알고리즘] 퀵 정렬(Quick Sort) (1) | 2021.07.19 |
| [알고리즘] 삽입 정렬 (Insertion Sort) (0) | 2021.07.18 |
| [알고리즘] 버블 정렬 (Bubble Sort) (0) | 2021.07.18 |



댓글