문제 출처 : https://www.acmicpc.net/problem/1922
1922번: 네트워크 연결
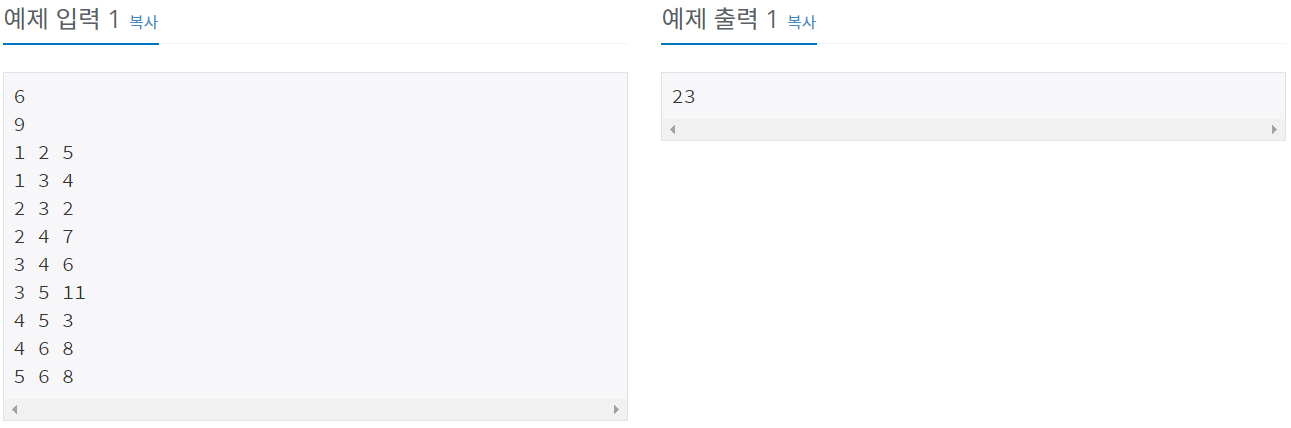
이 경우에 1-3, 2-3, 3-4, 4-5, 4-6을 연결하면 주어진 output이 나오게 된다.
www.acmicpc.net

문제
도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)
그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.
입력
첫째 줄에 컴퓨터의 수 N (1 ≤ N ≤ 1000)가 주어진다.
둘째 줄에는 연결할 수 있는 선의 수 M (1 ≤ M ≤ 100,000)가 주어진다.
셋째 줄부터 M+2번째 줄까지 총 M개의 줄에 각 컴퓨터를 연결하는데 드는 비용이 주어진다. 이 비용의 정보는 세 개의 정수로 주어지는데, 만약에 a b c 가 주어져 있다고 하면 a컴퓨터와 b컴퓨터를 연결하는데 비용이 c (1 ≤ c ≤ 10,000) 만큼 든다는 것을 의미한다. a와 b는 같을 수도 있다.
출력
모든 컴퓨터를 연결하는데 필요한 최소비용을 첫째 줄에 출력한다.
힌트
이 경우에 1-3, 2-3, 3-4, 4-5, 4-6을 연결하면 주어진 output이 나오게 된다.
알고리즘 분류
풀이
MST(최소 스패닝 트리)를 구하는 문제이며, 크루스칼, 프림 알고리즘으로 풀 수 있다.
크루스칼 알고리즘을 풀기 위해선 유니온 파인드 알고리즘에 대한 사전 지식이 필요하고,
프림 알고리즘은 다익스트라와 비슷한데, 꼭 다익스트라를 알지 못해도 괜찮다.
두 알고리즘의 완전한 기본 문제이므로, 크루스칼 알고리즘과 프림 알고리즘에 대해 학습한다면 그 코드 그대로 제출하면 될 것이다.
코드(크루스칼)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//1<=n <=1000
// 1<= m<= 100000
//1<= c<=10000
int n, m;
int parent[1001];
int result;
int getParent(int num) {
if (num == parent[num]) return num;
return parent[num] = getParent(parent[num]);
}
void unionParent(int a, int b) {
a = getParent(a);
b = getParent(b);
if (a != b) {
parent[a]= b;
}
}
bool findParent(int a, int b) {
a = getParent(a);
b = getParent(b);
if (a == b) {
return true;
}
else {
return false;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
vector<pair<int, pair<int, int>>> edge(m);
for (int i = 0; i < m; i++) {
int cost, a, b;
cin >> a >> b >> cost;
edge[i] = { cost,{a,b} };
}
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
sort(edge.begin(), edge.end());
for (int i = 0; i < m; i++) {
int cost = edge[i].first;
int a = edge[i].second.first;
int b = edge[i].second.second;
if (!findParent(a, b)) {
result += cost;
unionParent(a, b);
}
}
cout << result;
return 0;
}코드(프림)
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
//2<=n<=100000
//1<=m<=1000000
//<=가중치 <=1000
int n, m;
vector<pair<int,int>> edge[100001];
bool visited[100001];
int prim() {
priority_queue <pair<int, int>, vector<pair<int, int>>, greater<pair<int, int >>> pq;
int result=0;
pq.push( { 0,1 });
//visited[1] = true;
for (int i = 1; i <= n; i++) {
while (!pq.empty() &&visited[pq.top().second]) {
pq.pop();
}
int next = pq.top().second;
int minCost = pq.top().first;
visited[next] = true;
result += minCost;
for (auto o : edge[next]) {
pq.push({ o.second,o.first });
}
}
return result;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
edge[from].push_back({ to ,cost });
edge[to].push_back({ from,cost });
}
cout << prim();
return 0;
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 16508 전공책 c++ (조합) (0) | 2021.10.08 |
|---|---|
| 백준 1647 도시 분할 계획 c++ (MST) (0) | 2021.10.07 |
| 백준 16916 부분 문자열 c++ (kmp) (0) | 2021.10.07 |
| 백준 21608 상어 초등학교 c++ (구현) (0) | 2021.10.06 |
| 백준 10974 모든 순열 c++ (순열) (0) | 2021.10.05 |




댓글