참고 자료 : https://www.youtube.com/watch?v=qzfeVeajuyc

Topological Sort Result :
1 : 위상 정렬 가능(사이클이 존재하지 않는다.)
2 : 1, 2, 3, 5, 4, 6, 7 or 1, 2, 3, 4, 5, 6, 7
위상 정렬(Topological Sort)이란?
순서가 정해져 있는 작업을 차례대로 수행해야 할 때 사용하는 알고리즘으로,
방향 그래프에 존재하는 각 정점들의 선행 순서를 지키며 모든 정점을 나열하는 것이다.
위상 정렬(Topologicla Sort)의 특징
여러 개의 답이 존재할 수 있다.
그래프의 흐름은 '조건'이다.
사이클이 발생하는 경우 위상 정렬을 수행할 수 없다.
즉, DAG(Directed Acyclic Graph : 사이클이 존재하지 않는 방향 그래프)에서만 수행 가능하다.
시간 복잡도는 O(V+E) //V : Vertax(정점) E : Edge(간선)
위상 정렬(Topoligical Sort) 결과
1. 현재 그래프의 위상 정렬 가능 여부
2. 위상 정렬이 가능하다면, 그 결과 (위상 순서)
위상 정렬(Topoligical Sort) 구현 방법
※스택과 큐를 이용해서 구현할 수 있는데, 일반적으로 큐를 사용한다.
1. 진입 차수(inDegree)가 0인 정점을 큐에 삽입한다. //해당 정점을 가리키는 간선의 개수(진입 차수)
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
3. 간선 제거 이후에 진입 차수가 0이 된 정점을 큐에 삽입한다.
4. 큐가 빌 때까지 2~3번 과정을 반복한다.
//모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고,
//모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.
1.

| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 1 | 1 | 1 | 2 | 2 | 1 |
진입차수가 0인 정점 1을 큐에 삽입한다.(1번 과정)
2.

큐에 있던 정점 1을 꺼낸 뒤, 정점 1과 연결되어있던 간선들을 모두 제거한다.(2번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 1 | 1 | 1 | 2 | 1 |
3.

간선 제거 이후, 진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.(3번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 1 | 1 | 1 | 2 | 1 |
4.
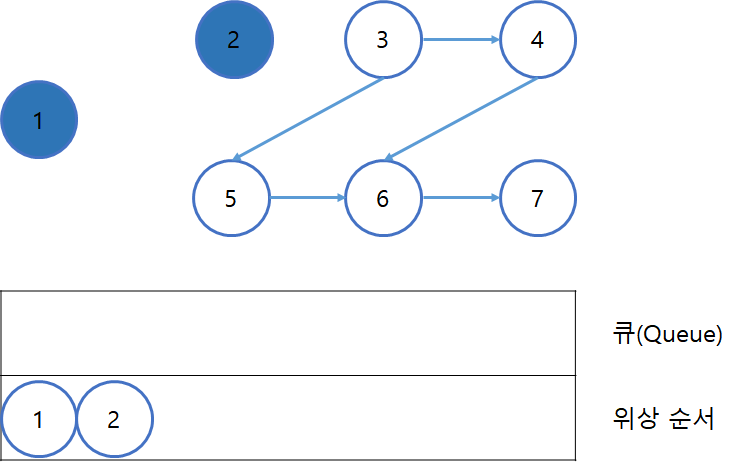
큐에 있던 정점 2를 꺼낸 뒤, 정점 2와 연결되어있던 간선들을 모두 제거한다.(2번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 1 | 1 | 2 | 1 |
5.

간선 제거 이후, 진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.(3번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 1 | 1 | 2 | 1 |
6.
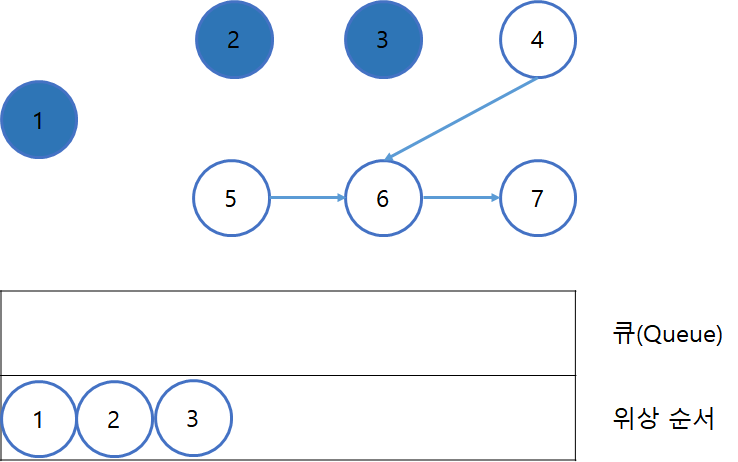
큐에 있던 정점 3을 꺼낸 뒤, 정점 3과 연결되어있던 간선들을 모두 제거한다.(2번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 2 | 1 |
7.
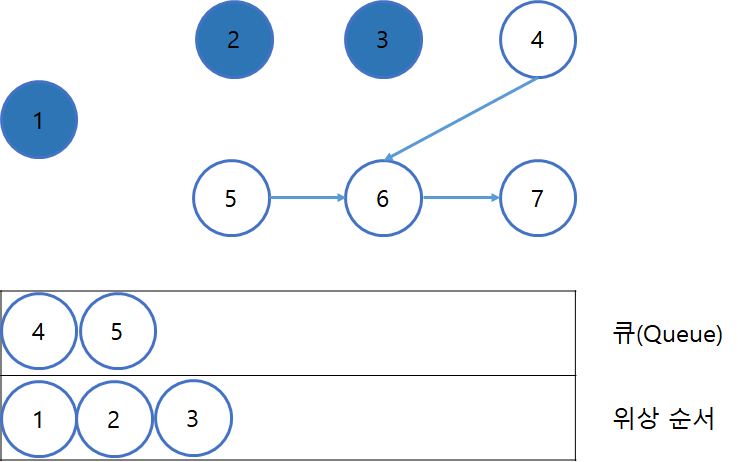
간선 제거 이후, 진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.(3번 과정)
//4번 5번의 순서는 바뀌어도 된다. -> 조건을 위배하지 않는 여러 개의 답이 존재한다.
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 2 | 1 |
8.

큐에 있던 정점 4,5를 꺼낸 뒤, 정점 4,5와 연결되어있던 간선들을 모두 제거한다.(2번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 0 | 1 |
9.
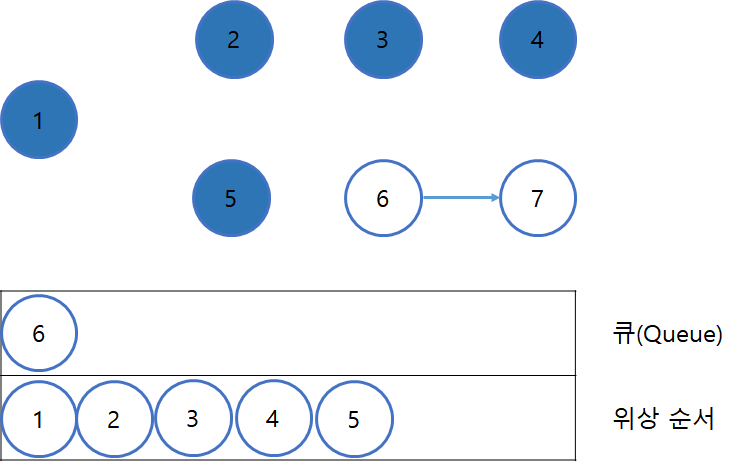
간선 제거 이후, 진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.(3번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 0 | 1 |
10.
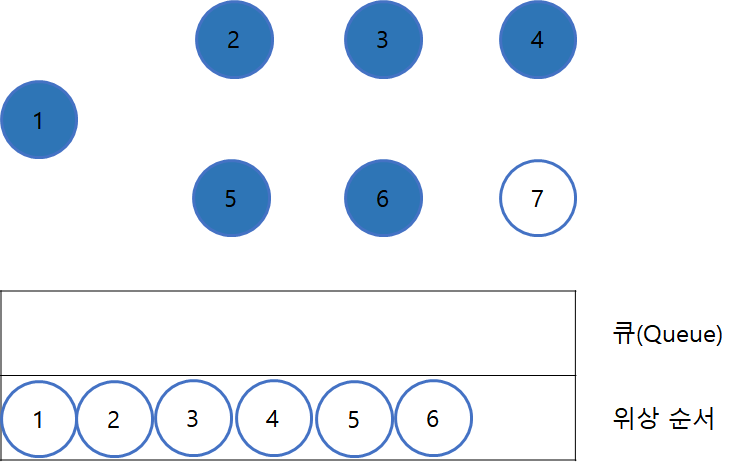
큐에 있던 정점 6을 꺼낸 뒤, 정점 6과 연결되어있던 간선들을 모두 제거한다.(2번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
11.

간선 제거 이후, 진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.(3번 과정)
| 정점 (node) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 (inDegree) |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
12.

큐에 있던 정점 7을 꺼낸 뒤, 정점 7과 연결되어 있던 간선들을 모두 제거한다.(2번 과정)
더 이상 진입차수가 0인 정점이 없으므로, 큐에 들어올 정점이 없기 때문에 위상 정렬을 종료한다.
모든 원소를 방문하기 전에 큐가 비었다면 사이클이 존재하므로, 위상 정렬을 끝까지 수행할 수 없었겠지만,
모든 원소를 방문한 후, 큐가 비었기 때문에 위상 정렬을 정상적으로 수행했다.
사이클이 존재하는 경우
사이클이 존재하는 그래프에 위상 정렬을 수행하면 어떻게 될까?
시작점을 알 수 없는 경우

| 정점 (node) |
1 | 2 | 5 | 6 |
| 진입차수 (inDegree) |
2 | 1 | 1 | 1 |
진입차수가 0인 정점이 없기 때문에 시작을 할 수 없다.
모든 정점을 방문할 수 없는 경우
1.

| 정점 (node) |
1 | 2 | 3 | 5 | 6 |
| 진입차수 (inDegree) |
0 | 2 | 1 | 1 | 1 |
2.

| 정점 (node) |
1 | 2 | 3 | 5 | 6 |
| 진입차수 (inDegree) |
0 | 1 | 1 | 0 | 1 |
이후, 정렬을 계속 진행해도 2번 정점의 진입차수가 0으로 줄지 않기 때문에,
2번, 3번 정점을 방문하지 않은 채 큐가 비어서 종료된다.
코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n = 7;//정점의 갯수
vector<int> edge[8]; //노드들의 간선을 저장 edge[1].push_back(2) == 1->2 방향의 간선
int inDegree[8]; //각 노드(정점)의 진입차수 저장
int result[8]; //결과(위상 순서)를 저장할 배열
void topologicalSort() {
queue<int> q;
for (int i = 1; i <= n; i++) {
if (inDegree[i] == 0)//진입차수가 0이면
q.push(i);//큐에 노드 삽입
}
for (int i = 1; i <= n; i++) {
if (q.empty()) { //모든 노드를 탐색하기 전에 큐가 빈다면 종료
cout << "그래프에 사이클이 존재합니다.\n";
return;
}
int cur_node = q.front();
q.pop(); //현재 노드를 큐에서 꺼내고
result[i] = cur_node;
for (int j = 0; j < edge[cur_node].size(); j++) { //큐에서 꺼낸 노드와 연결된 모든 간선 제거
int next_node = edge[cur_node][j];
if (--inDegree[next_node] == 0) { //간선을 제거한 다음 노드의 진입차수가 0이라면 큐에 저장
q.push(next_node);
}
}
}
for (int i = 1; i <= n; i++) { //결과(위상 순서)를 출력
cout << result[i] << ' ';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
//간선 정보 및 진입차수를 저장
edge[1].push_back(2);
inDegree[2]++;
edge[1].push_back(5);
inDegree[5]++;
edge[2].push_back(3);
inDegree[3]++;
edge[3].push_back(4);
inDegree[4]++;
edge[3].push_back(5);
inDegree[5]++;
edge[4].push_back(6);
inDegree[6]++;
edge[5].push_back(6);
inDegree[6]++;
edge[6].push_back(7);
inDegree[7]++;
//위상 정렬 실행
topologicalSort();
return 0;
}
위상 정렬 문제 풀어보기
해당 문제에선, 간선으로 연결된(먼저 푸는 것이 좋은 문제) 조건 외에, 가능하면 쉬운 문제부터(빠른 숫자부터) 풀어야 하는 조건이 있으므로, queue 대신 priority_queue(최소 힙)을 사용해야 한다.
ex)
1. 간선의 조건만 있으므로 큐를 사용한 위의 그래프
답 : 1, 2, 3, 5, 4, 6, 7 or 1, 2, 3, 4, 5, 6, 7
2. 간선의 조건 외에, 빠른 숫자부터 방문해야 한다는 조건이 추가된 경우
답 : 1, 2, 3, 4, 5, 6, 7
https://ongveloper.tistory.com/6
백준 1766 문제집 c++
문제 출처 : www.acmicpc.net/problem/1766 1766번: 문제집 첫째 줄에 문제의 수 N(1 ≤ N ≤ 32,000)과 먼저 푸는 것이 좋은 문제에 대한 정보의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에..
ongveloper.tistory.com
'알고리즘' 카테고리의 다른 글
| [알고리즘] 크루스칼(Kruskal)과 프림(Prim) (7) | 2021.12.15 |
|---|---|
| [알고리즘] 분할 정복(Divide and Conquer) (0) | 2021.07.21 |
| [알고리즘] 병합/합병 정렬(Merge Sort) (0) | 2021.07.21 |
| [알고리즘] 퀵 정렬(Quick Sort) (1) | 2021.07.19 |
| [알고리즘] 삽입 정렬 (Insertion Sort) (0) | 2021.07.18 |


댓글