문제 출처 : https://www.acmicpc.net/problem/21924
21924번: 도시 건설
첫 번째 줄에 건물의 개수 $N$ $(3 \le N \le 10^5 )$와 도로의 개수 $M$ $(2 \le M \le min( {N(N-1) \over 2}, 5×10^5)) $가 주어진다. 두 번째 줄 부터 $M + 1$줄까지 건물의 번호 $a$, $b$ $(1 \le a, b \le N, a ≠ b)$와 두
www.acmicpc.net

문제
채완이는 신도시에 건물 사이를 잇는 양방향 도로를 만들려는 공사 계획을 세웠다.
공사 계획을 검토하면서 비용이 생각보다 많이 드는 것을 확인했다.
채완이는 공사하는 데 드는 비용을 아끼려고 한다.
모든 건물이 도로를 통해 연결되도록 최소한의 도로를 만들려고 한다.
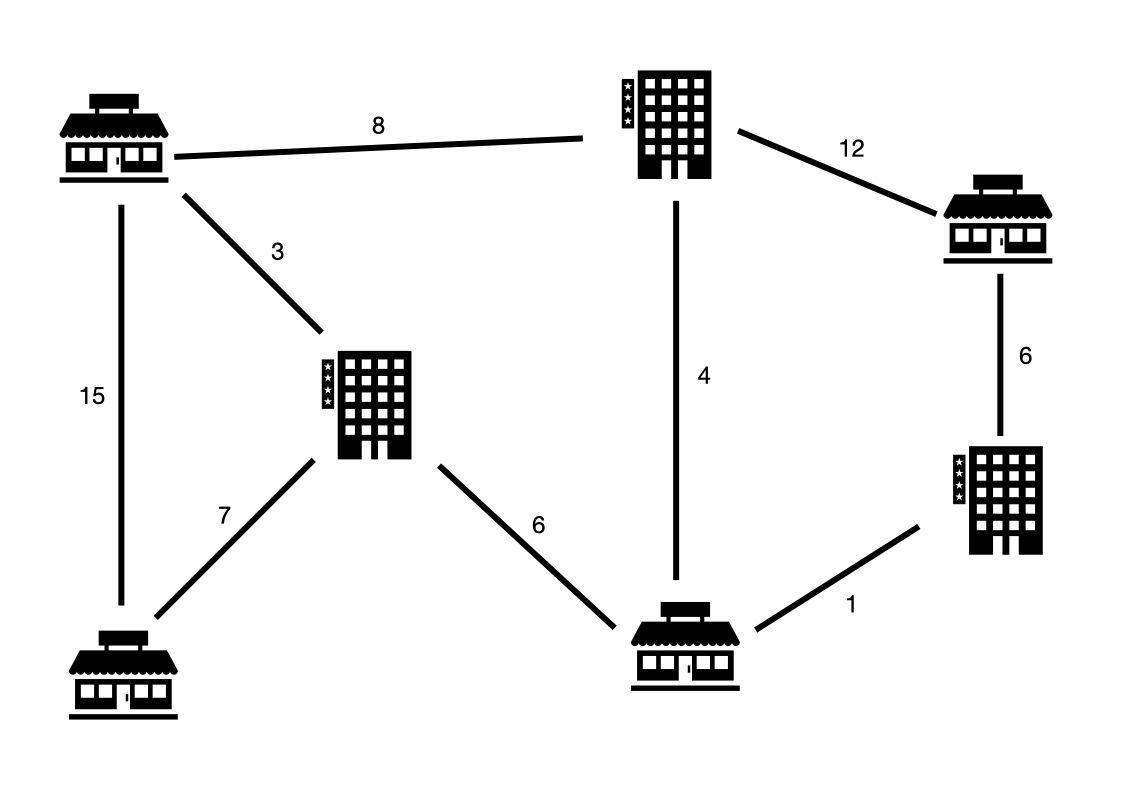
위 그림에서 건물과 직선으로 표시된 도로, 해당 도로를 만들 때 드는 비용을 표시해놓은 지도이다.

그림에 있는 도로를 다 설치할 때 드는 비용은 62이다. 모든 건물을 연결하는 도로만 만드는 비용은 27로 절약하는 비용은 35이다.
채완이는 도로가 너무 많아 절약되는 금액을 계산하는 데 어려움을 겪고 있다.
채완이를 대신해 얼마나 절약이 되는지 계산해주자.
입력
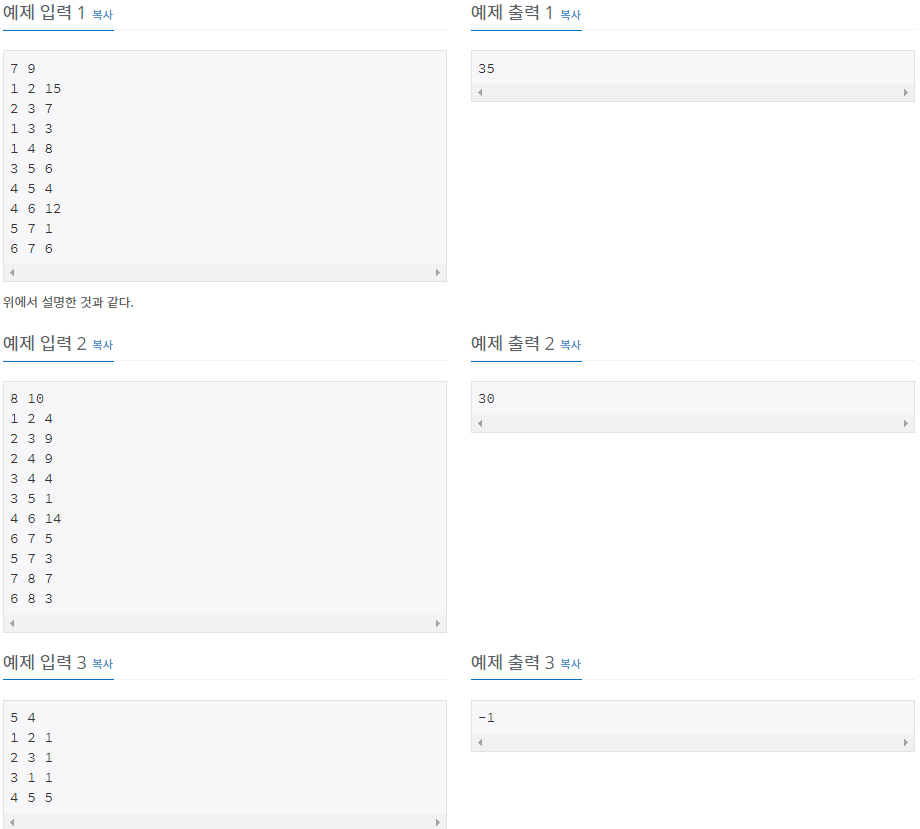
첫 번째 줄에 건물의 개수 N (3≤N≤105)와 도로의 개수 M (2≤M≤min(N(N−1)2,5×105))가 주어진다.
두 번째 줄 부터 M+1줄까지 건물의 번호 a, b (1≤a,b≤N,a≠b)와 두 건물 사이 도로를 만들 때 드는 비용 c(1≤c≤106)가 주어진다. 같은 쌍의 건물을 연결하는 두 도로는 주어지지 않는다.
출력
예산을 얼마나 절약 할 수 있는지 출력한다. 만약 모든 건물이 연결되어 있지 않는다면 -1을 출력한다.
알고리즘 분류
풀이
최소 스패닝 트리를 만드는 문제이다.
최소 스패닝 트리는 크루스칼 or 프림 알고리즘을 이용해 만들 수 있으며, 크루스칼 알고리즘은 유니온파인드 알고리즘을 이용해 만들 수 있다.
우선 주어진 간선을 비용의 오름차순으로 정렬한다.
비용이 낮은 간선부터 차례로 연결한다. 이때 연결은 두 노드의 부모 노드가 같지 않을 때만 UnionParent로 두 노드의 부모 노드를 합쳐주는 것으로 표현한다.
비용이 낮은 간선부터 연결했기 때문에, 모든 도시가 연결되면(최소 스패닝 트리) 남은 간선은 연결하지 않아도 되고,
절약한 비용을 계산하여 출력하면 된다. 만약 모든 노드의 부모 노드가 같지 않은 경우는 사이클이 발생하여 모든 노드를 연결할 수 없기 때문에 이때는 -1을 출력한다.
코드
import java.util.StringTokenizer
fun getParent(parent : IntArray, x : Int) : Int{
return if(parent[x]==x) x else getParent(parent,parent[x]).also { parent[x] = it }
}
fun findParent(parent : IntArray, a : Int, b : Int) : Boolean{
val aa = getParent(parent,a)
val bb = getParent(parent,b)
return if(aa==bb) true else false
}
fun unionParent(parent : IntArray, a : Int, b : Int){
val aa = getParent(parent,a)
val bb = getParent(parent,b)
if(aa<bb) parent[bb] = aa else parent[aa]=bb
}
fun main() = with(System.out.bufferedWriter()){
val br = System.`in`.bufferedReader()
var tk = StringTokenizer(br.readLine())
val (n,m) = List(2){Integer.parseInt(tk.nextToken())}
val graph = Array<Edge>(m){Edge(0,0,0)}
var sum =0L
var minSum=0L
val parent = IntArray(n+1)
for(i in 0 until m){
tk = StringTokenizer(br.readLine())
val (from, to, dis) = List(3){Integer.parseInt(tk.nextToken())}
graph[i]=Edge(from,to,dis)
sum +=dis
}
graph.sortWith(kotlin.Comparator{ a,b ->
when {
a.dis < b.dis -> -1
a.dis == b.dis -> 0
else -> 1
}
})
for(i in 1 .. n){
parent[i]=i
}
for(i in 0 until m) {
if (!findParent(parent, graph[i].from, graph[i].to)) {
minSum += graph[i].dis
unionParent(parent, graph[i].from, graph[i].to)
}
}
for(i in 2 .. n){
if(!findParent(parent,1,i)){
write("${-1}")
close()
return
}
}
write("${sum-minSum}")
close()
}
data class Edge(val from : Int, val to : Int, val dis : Int)
'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 9663 N-Queen Kotlin,c (백트래킹) (0) | 2021.09.02 |
|---|---|
| 백준 1389 케빈 베이컨의 6단계 법칙 Kotlin (플로이드 와샬) (0) | 2021.09.01 |
| 백준 3687 성냥개비 Kotlin (dp) (0) | 2021.09.01 |
| 백준 2015 수들의 합 4 Kotlin (누적 합) (0) | 2021.08.31 |
| 백준 1806 부분합 Kotlin (투 포인터) (0) | 2021.08.30 |




댓글