문제 출처 : https://www.acmicpc.net/problem/14722
14722번: 우유 도시
영학이는 딸기우유, 초코우유, 바나나우유를 좋아한다. 입맛이 매우 까다로운 영학이는 자신만의 우유를 마시는 규칙이 있다. 맨 처음에는 딸기우유를 한 팩 마신다. 딸기우유를 한 팩 마신 후
www.acmicpc.net

문제
영학이는 딸기우유, 초코우유, 바나나우유를 좋아한다.
입맛이 매우 까다로운 영학이는 자신만의 우유를 마시는 규칙이 있다.
- 맨 처음에는 딸기우유를 한 팩 마신다.
- 딸기우유를 한 팩 마신 후에는 초코우유를 한 팩 마신다.
- 초코우유를 한 팩 마신 후에는 바나나우유를 한 팩 마신다.
- 바나나우유를 한 팩 마신 후에는 딸기우유를 한 팩 마신다.
저번 축제에서 수많은 우유를 마셨지만 더욱 우유에 갈증을 느낀 영학이는 우유 여행을 떠났다.
맛있는 우유를 찾아 떠난 영학이는 수많은 우유 가게로 둘러 쌓인 어느 도시에 도착했다.
이 도시는 정사각형 형태의 2차원 격자 모양으로 남북으로 N개, 동서로 N개, 총 N*N개의 우유 가게들이 있다.
영학이는 도시의 서북쪽 끝 (1, 1)에서 출발해서 동남쪽 아래 (N, N)까지 까지 가면서 우유를 사 마신다.
각각의 우유 가게는 딸기, 초코, 바나나 중 한 종류의 우유만을 취급한다.
각각의 우유 가게 앞에서, 영학이는 우유를 사 마시거나, 사 마시지 않는다.
So cooooool~한 영학이는 오직 동쪽 또는 남쪽으로만 움직이기 때문에 한 번 지나친 우유 가게에는 다시 가지 않는다.
영학이가 마실 수 있는 우유의 최대 개수를 구하여라.
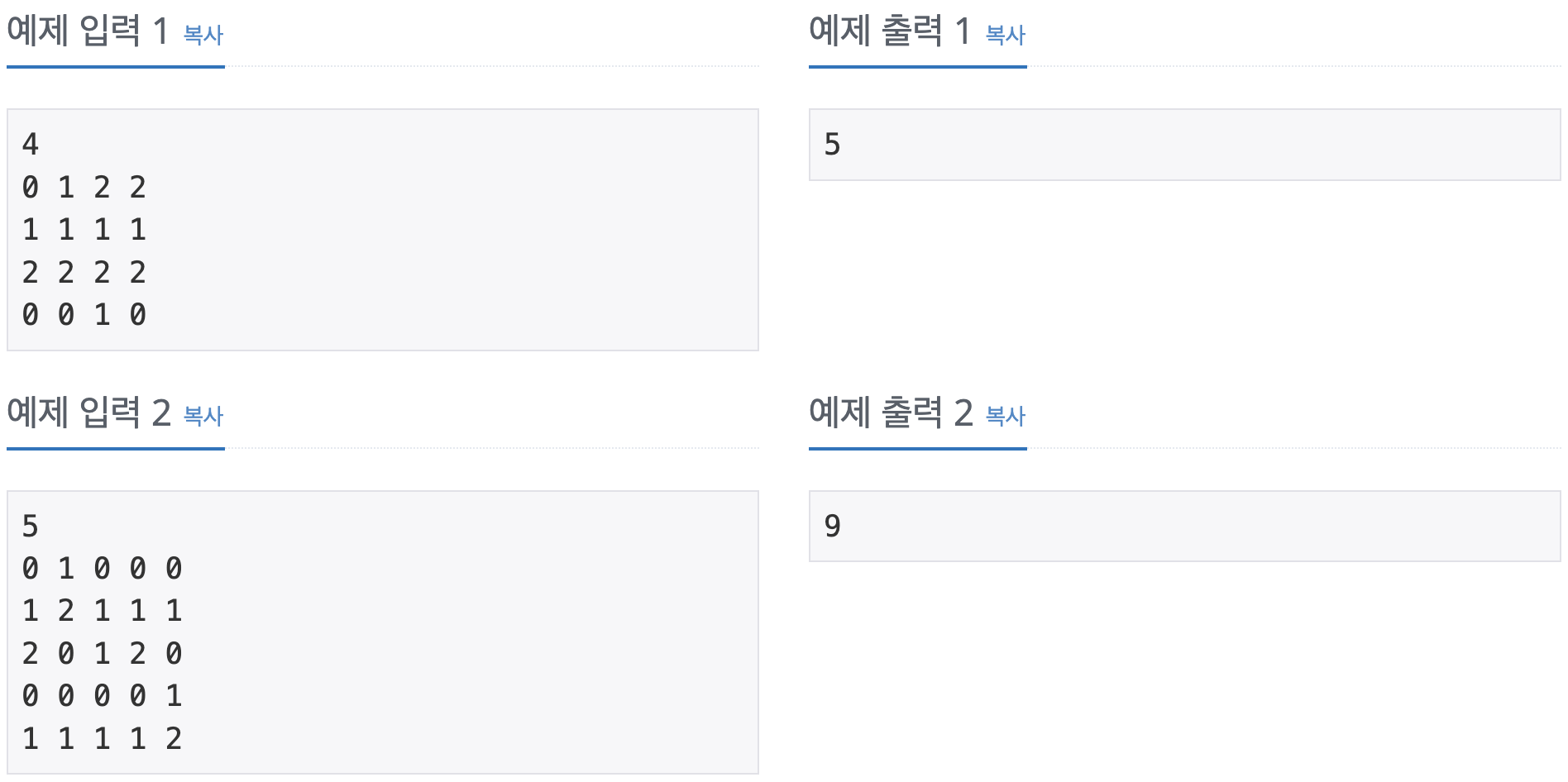
입력
첫 번째 줄에는 우유 도시의 영역 크기 N이 주어진다. (1 ≤ N ≤ 1000)
두 번째 줄부터 N+1 번째 줄까지 우유 도시의 정보가 주어진다.
0은 딸기우유만을 파는 가게, 1은 초코우유만을 파는 가게, 2는 바나나우유만을 파는 가게를 뜻하며, 0, 1, 2 외의 정수는 주어지지 않는다.
출력
영학이가 마실 수 있는 우유의 최대 개수를 출력하시오.
알고리즘 분류
풀이
dp 문제이다.
어떠한 칸에 도착했을 때, 우유를 먹을 수도, 안 먹을 수도 있다.
따라서 우,하 로 이동할 때 항상 연속적으로 우유를 먹어야 하는 것은 아니란 말이다.
0,0칸에서 먹고 그 이후로 안 먹다가 2,2칸에서 먹을 수 있기 때문에 단순히 이전 칸의 우유를 확인하는 게 아니라, 이전 칸에서 어떤 우유를 먹은 상태인지 확인해야 한다는 의미이다.
따라서 3차원 dp가 필요하다.
dp[milk][r][c] = r,c 좌표까지 도달하는 데 가장 최근에 먹은 우유는 milk일 때의 최대로 먹은 우유 개수
안 먹는 경우 : 그냥 안 먹거나, 못 먹는 경우이거나,
먹는 경우 : 먹을 수 있거나, 먹을 수 없거나
우선 우유를 먹는 경우를 생각해 보자.
이전 2번 우유를 먹으려면 이전 칸에서 1번 우유를 먹은 상태여야 한다.
먹은 상태여야 한단 말이 좀 중요한데,
| 1 | 1 |
| 1 | 2 |
위 그래프에서 2번 우유는 먹을 수 없다. 왜냐면 이전 칸이 1이지만 0번 우유를 먹은 적이 없어서 1번 우유를 먹은 상태일 수가 없기 때문이다.
| 0 | 1 |
| 1 | 2 |
위 그래프에서 2번 우유는 먹을 수 있다. 이전 칸이 1인 것은 동일한데, 전전 0인 칸에서 0을 먹을 수 있기 때문에 이전 칸에서 1번 우유를 먹은 상태일 수 있다.
우유를 먹은 상태인 것을 어떻게 알 수 있을까? 우리가 설계한 dp 배열을 통해 알 수 있다.
dp[이전 우유][이전 칸][이전 칸] > 0 인 경우에만 이전 칸의 가장 최근 우유(위에서 말한 이전 우유) 상태이다.
dp[이전 우유][이전 칸][이전 칸] == 0인 경우는 이전 칸에 이전 우유를 먹은 상태로 도달할 수 없음을 의미한다.
따라서 우유를 먹을 때의 점화식은 다음과 같다.
//우유 먹는 경우 (이전 칸에서 최근에 먹은 우유가 beforeMilk일 때 값이 1이상이라면 우유 이어서 먹을 수 있음)
if (dp[beforeMilk][beforeR][beforeC] > 0) {
dp[curMilk][r][c] = dp[curMilk][r][c].coerceAtLeast(dp[beforeMilk][beforeR][beforeC] + 1)
}우유를 안 먹을 땐? 안 먹으니까 무조건 dp 값은 0일까?
아니다. 어떠한 좌표 r,c칸에 도달할 때 r,c 칸의 우유를 먹지 않더라도 r,c칸까지 도착하는 데 마신 우유의 최댓값을 구해야 하기 때문에 이전 값을 그대로 들고 와야 한다. 이미 r,c칸에 최대 개수가 들어있다면 스킵
따라서 우유를 안 먹을 때의 점화식은 다음과 같다.
//우유 안 먹는 경우
dp[0][r][c] = dp[0][r][c].coerceAtLeast(dp[0][beforeR][beforeC])
dp[1][r][c] = dp[1][r][c].coerceAtLeast(dp[1][beforeR][beforeC])
dp[2][r][c] = dp[2][r][c].coerceAtLeast(dp[2][beforeR][beforeC])
추가적으로 초기값 설정은 0번 우유인 칸들은 앞에 우유를 하나도 먹지 않으면 무조건 먹을 수 있기 때문에 미리
dp[0][0번 우유 r][0번 우유 c] = 1로 처리해 둔다.
나머진 2중 포문 안에 이전 좌표 탐색하는 사이즈 2의 포문 하나 추가해서 총 3개의 포문이지만 사이즈 2의 포문은 무시하고
O(N^2)의 시간 복잡도 풀이이다. (사이즈 2 포문은 선택이다. 보일러 플레이트 코드 때문에 예쁘게 for문으로 했는데 그냥 왼, 위 칸 좌표 하드코딩 해도 된다.)
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
fun getInt() = br.readLine().trim().toInt()
lateinit var graph: Array<List<Int>>
lateinit var dp: Array<Array<IntArray>>
val dir = arrayOf(
arrayOf(0, -1),
arrayOf(-1, 0),
)
fun main() = with(System.out.bufferedWriter()) {
//input
val n = getInt()
dp = Array(3) { Array(n) { IntArray(n) } }
graph = Array(n) { r ->
val list = getIntList()
list.forEachIndexed { c, value ->
//0인 칸은 이전 칸들에서 하나도 안 먹고 오면 우유 먹을 수 있으니 무조건 1
if (value == 0) dp[0][r][c] = 1
}
list
}
//solve
for (r in 0 until n) {
for (c in 0 until n) {
for (i in dir.indices) {
val beforeR = r + dir[i][0]
val beforeC = c + dir[i][1]
if (beforeR !in 0 until n || beforeC !in 0 until n) continue
val curMilk = graph[r][c]
val beforeMilk = (curMilk + 2) % 3
//우유 안 먹는 경우
dp[0][r][c] = dp[0][r][c].coerceAtLeast(dp[0][beforeR][beforeC])
dp[1][r][c] = dp[1][r][c].coerceAtLeast(dp[1][beforeR][beforeC])
dp[2][r][c] = dp[2][r][c].coerceAtLeast(dp[2][beforeR][beforeC])
//우유 먹는 경우 (이전 칸에서 최근에 먹은 우유가 beforeMilk일 때 값이 1이상이라면 우유 이어서 먹을 수 있음)
if (dp[beforeMilk][beforeR][beforeC] > 0) {
dp[curMilk][r][c] = dp[curMilk][r][c].coerceAtLeast(dp[beforeMilk][beforeR][beforeC] + 1)
}
}
}
}
//output
val answer = dp[0][n - 1][n - 1].coerceAtLeast(dp[1][n - 1][n - 1]).coerceAtLeast(dp[2][n - 1][n - 1])
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 17141 연구소 2 Kotlin (그래프) (0) | 2023.03.12 |
|---|---|
| 백준 16194 카드 구매하기 2 Kotlin (dp) (0) | 2023.03.12 |
| 백준 11060 점프 점프 Kotlin (dp) (0) | 2023.02.19 |
| 백준 20208 진우의 민트초코우유 Kotlin (백트래킹) (0) | 2023.02.12 |
| 백준 2922 즐거운 단어 Kotlin (백트래킹) (0) | 2023.02.10 |




댓글