문제 출처: https://www.acmicpc.net/problem/17141
17141번: 연구소 2
인체에 치명적인 바이러스를 연구하던 연구소에 승원이가 침입했고, 바이러스를 유출하려고 한다. 승원이는 연구소의 특정 위치에 바이러스 M개를 놓을 것이고, 승원이의 신호와 동시에 바이
www.acmicpc.net

문제
인체에 치명적인 바이러스를 연구하던 연구소에 승원이가 침입했고, 바이러스를 유출하려고 한다. 승원이는 연구소의 특정 위치에 바이러스 M개를 놓을 것이고, 승원이의 신호와 동시에 바이러스는 퍼지게 된다.
연구소는 크기가 N×N인 정사각형으로 나타낼 수 있으며, 정사각형은 1×1 크기의 정사각형으로 나누어져 있다. 연구소는 빈 칸, 벽으로 이루어져 있으며, 벽은 칸 하나를 가득 차지한다.
일부 빈 칸은 바이러스를 놓을 수 있는 칸이다. 바이러스는 상하좌우로 인접한 모든 빈 칸으로 동시에 복제되며, 1초가 걸린다.
예를 들어, 아래와 같이 연구소가 생긴 경우를 살펴보자. 0은 빈 칸, 1은 벽, 2는 바이러스를 놓을 수 있는 칸이다.
2 0 0 0 1 1 0
0 0 1 0 1 2 0
0 1 1 0 1 0 0
0 1 0 0 0 0 0
0 0 0 2 0 1 1
0 1 0 0 0 0 0
2 1 0 0 0 0 2M = 3이고, 바이러스를 아래와 같이 놓은 경우 6초면 모든 칸에 바이러스를 퍼뜨릴 수 있다. 벽은 -, 바이러스를 놓은 위치는 0, 빈 칸은 바이러스가 퍼지는 시간으로 표시했다.
6 6 5 4 - - 2
5 6 - 3 - 0 1
4 - - 2 - 1 2
3 - 2 1 2 2 3
2 2 1 0 1 - -
1 - 2 1 2 3 4
0 - 3 2 3 4 5시간이 최소가 되는 방법은 아래와 같고, 5초만에 모든 칸에 바이러스를 퍼뜨릴 수 있다.
0 1 2 3 - - 2
1 2 - 3 - 0 1
2 - - 2 - 1 2
3 - 2 1 2 2 3
3 2 1 0 1 - -
4 - 2 1 2 3 4
5 - 3 2 3 4 5연구소의 상태가 주어졌을 때, 모든 빈 칸에 바이러스를 퍼뜨리는 최소 시간을 구해보자.
입력
첫째 줄에 연구소의 크기 N(5 ≤ N ≤ 50), 놓을 수 있는 바이러스의 개수 M(1 ≤ M ≤ 10)이 주어진다.
둘째 줄부터 N개의 줄에 연구소의 상태가 주어진다. 0은 빈 칸, 1은 벽, 2는 바이러스를 놓을 수 있는 칸이다. 2의 개수는 M보다 크거나 같고, 10보다 작거나 같은 자연수이다.
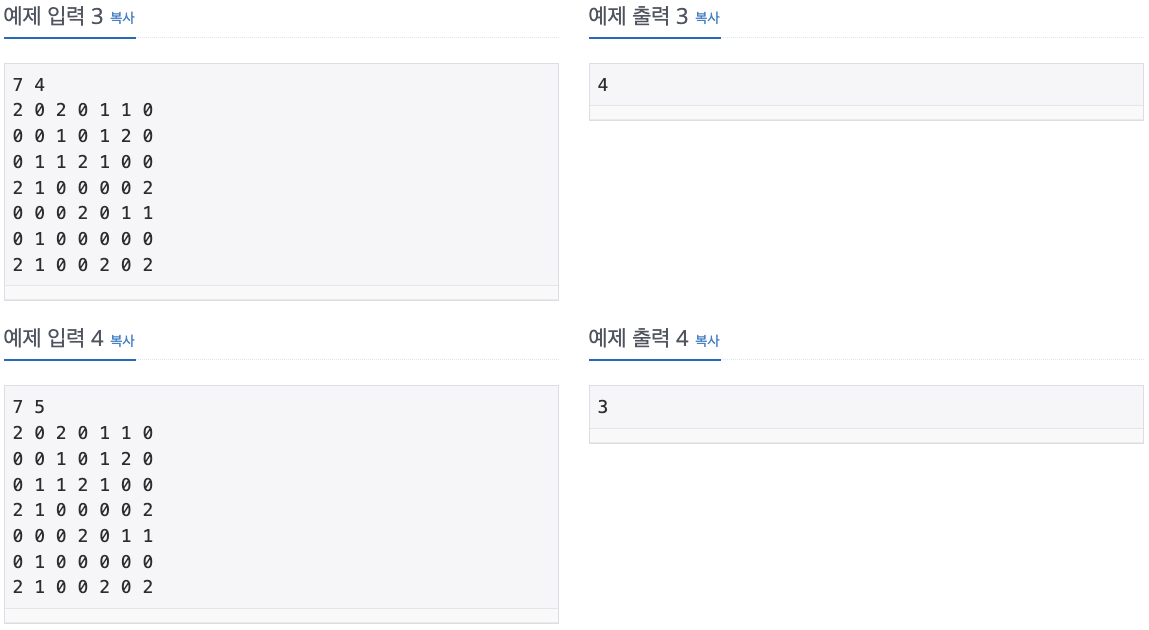
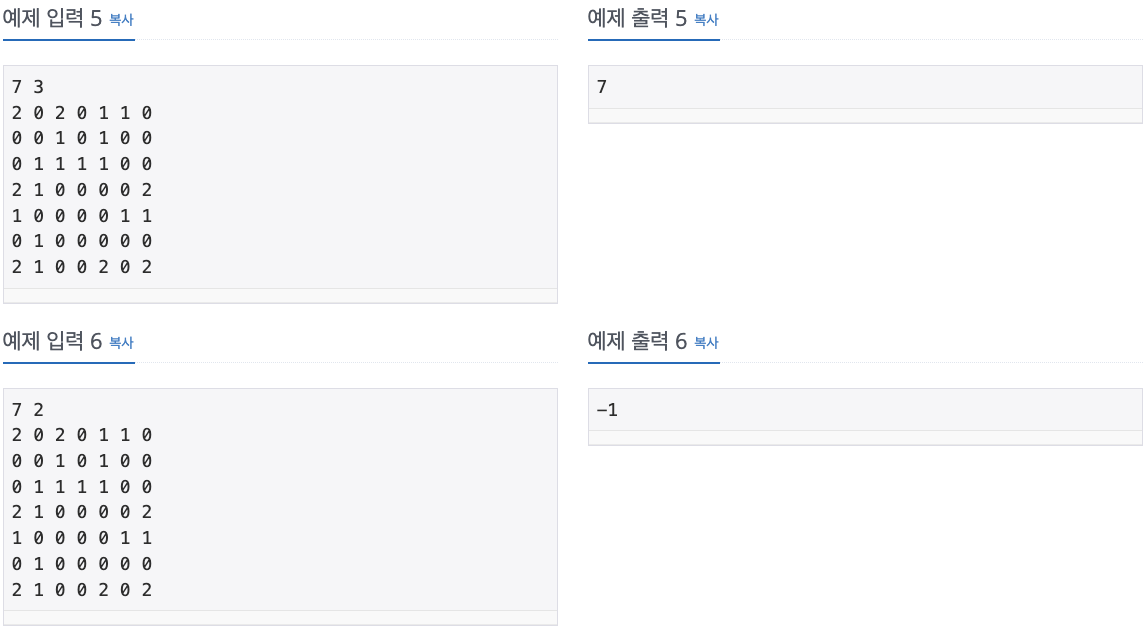
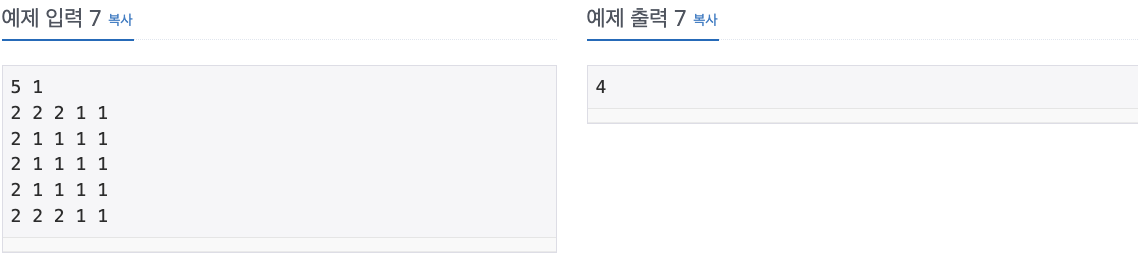
출력
연구소의 모든 빈 칸에 바이러스가 있게 되는 최소 시간을 출력한다. 바이러스를 어떻게 놓아도 모든 빈 칸에 바이러스를 퍼뜨릴 수 없는 경우에는 -1을 출력한다.

알고리즘 분류
풀이
그래프 탐색 문제이다.
바이러스가 처음 들어갈 수 있는 공간은 총 10칸, 바이러스의 최대 개수는 10개
즉 10C1~10의 조합으로 바이러스를 배치하는 모든 경우의 수를 찾을 수 있다.
전체적인 풀이는 다음과 같다.
1. 10Cm으로 바이러스를 배치하는 모든 경우의 수를 찾는다.
2. 각 경우의 수마다 그래프 탐색을 돌린다 (bfs)
3. 매 초마다 현재 큐의 사이즈를 이용해 큐의 사이즈만큼만 bfs를 돌리는 것으로 매 초마다 그래프 상태를 구할 수 있다.
3.1 그래프는 당연히 임시 그래프를 만들어서 사용한다. (바이러스를 다르게 배치하는 경우 다시 초기 그래프 상태에서 시작해야 한다.)
4. 본인은 바이러스가 지나간 칸을 1로 표현했다. 즉 매 초마다 탐색을 마치고 (바이러스 퍼트리기) 그래프에서 1의 개수가 n*n과 같은지 확인한다.
주의할 점은 바이러스를 배치했는데 모든 칸이 바이러스 혹은 벽인 경우이다.
이 경우에는 0이 답이 나와야한다.
두 가지 예시를 생각해 보자.
5 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 2 2 1
answer = 1
5 2
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 2 2 1
answer = 2코드
import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
lateinit var graph: Array<IntArray>
val virusPlaces = ArrayList<Pair<Int, Int>>()
var answer = Int.MAX_VALUE
val dir = arrayOf(
arrayOf(0,1),
arrayOf(1,0),
arrayOf(0,-1),
arrayOf(-1,0),
)
fun main() = with(System.out.bufferedWriter()) {
//input
val (n, m) = getIntList()
graph = Array(n) { r ->
val list = getIntList()
for (c in list.indices) {
if (list[c] == 2) {
virusPlaces.add(Pair(r, c))
}
}
list.toIntArray()
}
//solve
virusCombination(IntArray(m),0, 0, n, m)
//output
write("${if(answer == Int.MAX_VALUE) -1 else answer}")
close()
}
fun virusCombination(selectedVirusPlaces: IntArray, idx: Int, cnt: Int, n: Int, m: Int) {
if(cnt == m){
answer = answer.coerceAtMost(play(selectedVirusPlaces,n,m))
return
}
for (i in idx until virusPlaces.size) {
selectedVirusPlaces[cnt]= i
virusCombination(selectedVirusPlaces, i+1, cnt+1, n,m)
}
}
fun play(selectedVirusPlaces: IntArray, n: Int, m: Int): Int {
val q: Queue<Pair<Int,Int>> = LinkedList()
var time = 0
val tempGraph = Array(n){ r->
IntArray(n){c->
graph[r][c]
}
}
for(i in selectedVirusPlaces){
val (r,c) = virusPlaces[i]
q.add(virusPlaces[i])
tempGraph[r][c] = 1
}
if(checkFinish(tempGraph,n)) return time
while(q.isNotEmpty()){
val size = q.size
time++
for(i in 0 until size) {
val (cr,cc) = q.poll()
for(j in 0 until 4){
val nr = cr + dir[j][0]
val nc = cc + dir[j][1]
if(nr !in 0 until n || nc !in 0 until n) continue
if(tempGraph[nr][nc] == 1) continue
tempGraph[nr][nc] = 1
q.add(Pair(nr,nc))
}
}
if(checkFinish(tempGraph,n)) return time
}
return Int.MAX_VALUE
}
fun checkFinish(tempGraph: Array<IntArray>, n: Int): Boolean{
var wallCnt = 0
for(r in 0 until n){
for(c in 0 until n){
if(tempGraph[r][c] == 1) wallCnt++
}
}
return wallCnt==n*n
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 13397 구간 나누기 2 Kotlin (파라메트릭 서치) (0) | 2023.03.19 |
|---|---|
| 백준 9084 동전 Kotlin (dp) (0) | 2023.03.19 |
| 백준 16194 카드 구매하기 2 Kotlin (dp) (0) | 2023.03.12 |
| 백준 14722 우유 도시 Kotlin (dp) (0) | 2023.02.19 |
| 백준 11060 점프 점프 Kotlin (dp) (0) | 2023.02.19 |




댓글