문제 출처 : https://www.acmicpc.net/problem/5639
5639번: 이진 검색 트리
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다
www.acmicpc.net

문제
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
- 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
- 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
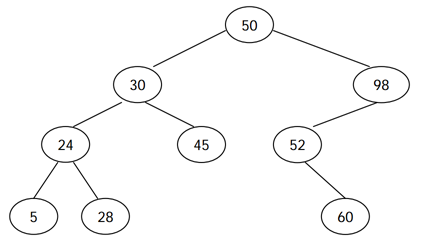
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.

알고리즘 분류
풀이
트리의 전위 순회(루트, 왼, 오) 결과가 입력으로 주어졌을 때, 이를 가지고 후위 순회(왼, 오, 루트) 결과를 출력하는 문제이다. 우선 전위 순휘를 나열해보면
| 50 | 30 | 24 | 5 | 28 | 45 | 98 | 52 | 60 |
이와 같은데, 전위 순회에서 루트노드는 50이 될 것이고, 루트 노드보다 큰 값이 나오기 전까지는 모두 루트 노드의 왼쪽 자식들일 것이다. 이를 다시 나타내면 다음과 같다.
root
left
right
| 50 | 30 | 24 | 5 | 28 | 45 | 98 | 52 | 60 |
후위 연산은 left, right, root 순이기 때문에 이 순서대로 재귀를 돌려주면 후위 연산의 결과를 출력할 수 있다.
코드
#include <iostream>
#include <vector>
using namespace std;
//0<= node <=10000
int tree[10000];
void postOrder(int start, int end) {
if (start >= end) {
return;
}
if (start == end - 1) {
cout << tree[start] << '\n';
return;
}
int idx = start + 1;
while (idx<end) {
if (tree[start]<tree[idx]) {
break;
}
idx++;
}
postOrder(start+1, idx);
postOrder(idx, end);
cout << tree[start] << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int num;
int inputIdx = 0;
while (cin >> num) {
tree[inputIdx++] = num;
}
postOrder(0,inputIdx);
return 0;
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 1654 랜선 자르기 c++, Kotlin (이분 탐색) 2022-06-26 코틀린 추가 (0) | 2021.10.14 |
|---|---|
| 백준 18352 특정 거리의 도시 찾기 c++ (bfs) (0) | 2021.10.13 |
| 백준 12919 A와 B 2 c++ (투 포인터) 2022-06-20 코틀린 추가 (0) | 2021.10.11 |
| 백준 1991 트리 순회 c++ (트리) (0) | 2021.10.10 |
| 백준 1789 수들의 합 c++ (이분 탐색) (0) | 2021.10.10 |




댓글