문제 출처 : https://www.acmicpc.net/problem/20181
20181번: 꿈틀꿈틀 호석 애벌레 - 효율성
꿈틀꿈틀 호석 애벌레는 N 개의 먹이가 일렬로 나열된 나뭇가지를 오른쪽으로 기어가려고 한다. 시작하는 순간의 호석 애벌레가 0의 위치에 있고 i 번째 먹이는 오른쪽으로 i 초 기어가야 도달할
www.acmicpc.net

문제
꿈틀꿈틀 호석 애벌레는 N 개의 먹이가 일렬로 나열된 나뭇가지를 오른쪽으로 기어가려고 한다. 시작하는 순간의 호석 애벌레가 0의 위치에 있고 i 번째 먹이는 오른쪽으로 i 초 기어가야 도달할 수 있다. 또한 매초 1 만큼 오른쪽으로 무조건 진행한다.
호석 애벌레는 i 번째 먹이가 맛있을수록 높은 만족도를 얻는다. 호석 애벌레는 절제라는 것을 모르는 욕심쟁이기 때문에 한번 먹이를 먹기 시작하면 연속적으로 계속 먹어야 하며, 누적된 만족도가 최소 만족도 K 이상이 되거나 더 이상 먹을 먹이가 없을 때에 연속적으로 먹는 것을 멈춘다. 만약 최소 만족도 이상이 되면 K 를 초과한 만족도만큼 탈피 에너지를 축적한다. 직후에 호석 애벌레의 만족도는 다시 0 이 되고 먹이를 먹을 수 있게 된다. 나뭇가지를 전부 통과했을 때에 소화를 다 못 했을 경우에도 탈피 에너지는 최소 만족도를 넘기는 순간 이미 축적한 것으로 생각하자.
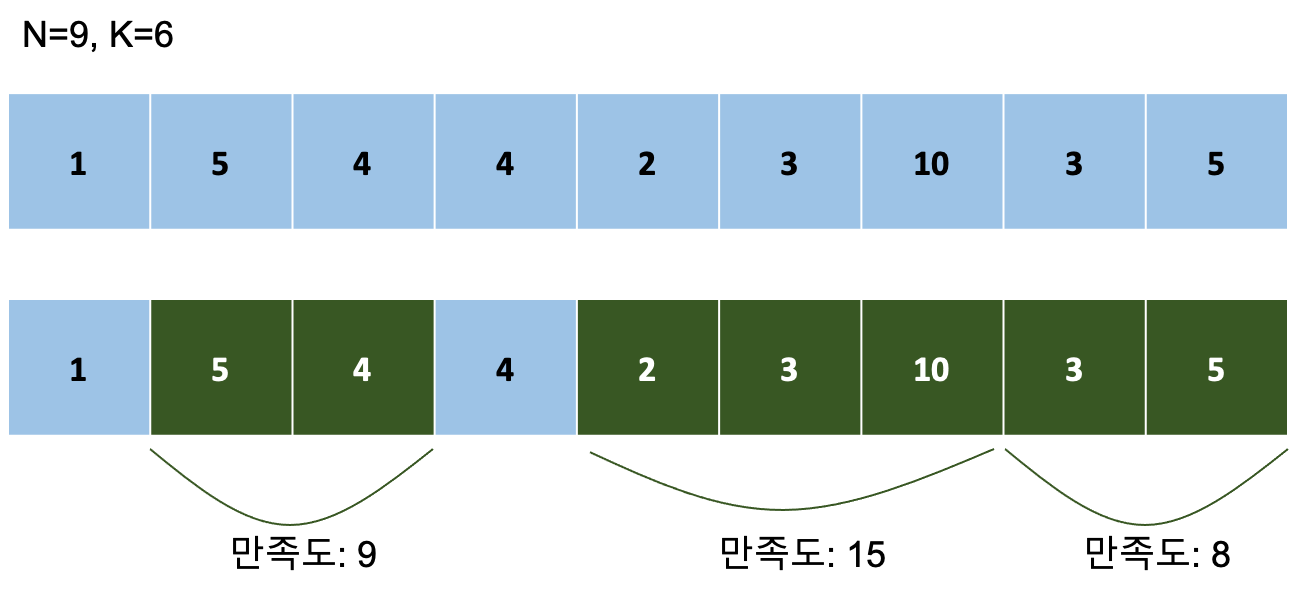
예를 들어 위와 같이 9개의 먹이가 존재하면, 호석 애벌레는 미래를 도모하여 1번 먹이를 과감하게 포기한다. 그리고 2번부터 먹기 시작해서 3번까지 먹으면 만족도가 9가 되어 3의 에너지를 축적하게 된다. 같은 이유로 4번 먹이도 포기하고 5번부터 먹으면 7번까지 연속으로 먹어서 15의 만족도를 얻는다. 이를 통해 9의 탈피 에너지가 쌓인다. 8, 9번 먹이까지 먹게 되면 2의 탈피 에너지가 축적된다. 이렇게 얻은 총 14의 탈피 에너지가 위의 예제에서는 최대치이다.
매초마다 호석 애벌레는 오른쪽으로 이동하면서 먹이를 지나치거나 먹기 시작할 수 있다. 먹기 시작하면 만족도가 채워질때까지 먹게 될것이다. 어떤 먹이들을 대해 먹어야 축적된 탈피 에너지가 최대가 될 수 있을까?
입력
첫번째 줄에 먹이 개수 N, 최소 만족도 K 가 공백으로 주어진다.
두번째 줄에는 1 번부터 N 번 먹이의 만족도가 순서대로 주어진다.
출력
축적된 탈피 에너지의 최댓값을 구하라. 만약 탈피를 한 번도 할 수 없다면 0을 출력한다.
제한
- 1 ≤ N ≤ 100,000, N 은 정수이다.
- 1 ≤ K ≤ 108, K 는 정수이다.
- 0 ≤ 각 먹이의 만족도 ≤ 108, 모든 만족도는 정수이다.
알고리즘 분류
풀이
2022.05.17 - [알고리즘 문제 풀이/백준] - 백준 20167 꿈틀꿈틀 호석 애벌레 - 기능성 Kotlin (완전 탐색)
위 문제의 확장판이다.
N의 크기가 20에서 10만으로 늘었고, k도 1억으로 늘었다.
이전 풀이는 현재 칸을 먹기 vs 안 먹기로 매 칸마다 2개의 선택지가 있었으니, 같은 풀이로 접근하면 10만^2로 시간 초과가 뜬다.
본인은 이를 dp + 투 포인터로 해결하였다.
이전엔 그냥 직관적으로 한 칸씩 모두 탐색했지만, 이 문제는 결국 구간을 다루는 문제이다.
어떠한 구간 a칸부터 b칸까지 먹었을 때의 만족도들을 계산하여 최대 만족도를 얻는 경우를 찾아야 하고, a와 b를 적절히 선택함으로써 구할 수 있다. 그럼 이 구간 a~b를 어떻게 최적의 구간으로 만들지가 관건인데, 이때 투 포인터와 dp를 사용할 수 있다.
우선 만족도가 Int의 범위를 초과할 수 있으므로 Long타입으로 바꾸어주고,
구간 a b를 설정하기 위해 두 개의 포인터 s,e를 둔다.
s는 a를 의미하는 start
e는 b를 의미하는 end
인덱스이다.
sum에 s+1부터 e까지의 만족도 합을 누적한다.
이 sum이 k이상이라면
dp[e] = dp[e] vs dp[s] + (sum-k)
위의 식으로 dp[e]값을 최신화한다.
//dp[e] = e까지 확인해봤을 때 누적도의 최댓값
위 식의 의미는 s+1부터 e까지 먹었을 때의 값(sum-k)와 현재 s+1 ~ e 범위 이전까지 구했던 최댓값을 더해서 0부터 e까지 확인했을 때의 전체적인 최댓값으로 갱신하겠단 의미이다.
말이 어려운데 이 부분은 코드를 보면 더 와닿을 것이다.
무튼 sum이 k이상일 때는 위의 작업을 sum이 k보다 작아질 때까지 s를 늘려가며 sum값을 줄여주면서 반복한다.
sum이 k보다 작을 때에는
dp[e] = Max(dp[e-1], dp[e])로 앞에서 나왔던 최댓값 결과를 계속 가져온다.
내가 봐도 이 글은 투 포인터와 dp에 대한 지식이 없는 상태로 보면 화가 많이 날 것 같다.
진정하고 투 포인터와 dp 개념부터 공부하고 본다면 좀 이해가 될 것이다.
코드
import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
lateinit var graph: List<Long>
lateinit var dp: LongArray
fun main() = with(System.out.bufferedWriter()){
//input
val (n, k) = getIntList()
val tk = StringTokenizer(br.readLine())
graph = List(n+1){
if(it==0)
0
else
tk.nextToken().toLong()
}
dp = LongArray(n+1)
//solve
//twoPointer
var s = 0
var sum = 0L
for(e in 1 .. n){
sum += graph[e]
dp[e] = dp[e].coerceAtLeast(dp[e-1])
while(sum >= k){
dp[e] = dp[e].coerceAtLeast(dp[s] + sum-k)
sum -= graph[++s]
}
}
//output
write("${dp[n]}")
close()
}
'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 11779 최소비용 구하기 2 Kotlin (다익스트라) (0) | 2022.05.18 |
|---|---|
| 백준 20167 꿈틀꿈틀 호석 애벌레 - 기능성 Kotlin (완전 탐색) (0) | 2022.05.17 |
| 백준 17069 파이프 옮기기 2 Kotlin (dp) (0) | 2022.05.15 |
| 백준 20183 골목 대장 호석 - 효율성 2 Kotlin (다익스트라 + 이분 탐색) (0) | 2022.05.14 |
| 백준 20182 골목 대장 호석 - 효율성 1 Kotlin (다익스트라 + 이분 탐색) (0) | 2022.05.12 |




댓글