문제 출처 : https://www.acmicpc.net/problem/15681
15681번: 트리와 쿼리
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105) 이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
www.acmicpc.net

문제
간선에 가중치와 방향성이 없는 임의의 루트 있는 트리가 주어졌을 때, 아래의 쿼리에 답해보도록 하자.
- 정점 U를 루트로 하는 서브트리에 속한 정점의 수를 출력한다.
만약 이 문제를 해결하는 데에 어려움이 있다면, 하단의 힌트에 첨부한 문서를 참고하자.
입력
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105)
이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
이는 U와 V를 양 끝점으로 하는 간선이 트리에 속함을 의미한다.
이어 Q줄에 걸쳐, 문제에 설명한 U가 하나씩 주어진다. (1 ≤ U ≤ N)
입력으로 주어지는 트리는 항상 올바른 트리임이 보장된다.
출력
Q줄에 걸쳐 각 쿼리의 답을 정수 하나로 출력한다.

힌트

그래프란, 정점들과 정점 둘을 잇는 간선들로 이루어진 집합을 의미한다.
위는 9개의 정점(원 모양)과, 10개의 간선(실선) 들로 이루어진 그래프이다. 각 원의 내부에 쓰여 있는 숫자는 편의상 정점에 매긴 번호를 의미한다.
붉은 간선은 차후 설명의 편의상 색칠해 둔 것으로, 우선은 다른 검은 간선과 동일한 것으로 간주하도록 하자.
간선은 항상 두 정점을 잇게 된다. 이제부터의 설명에서는, 각 정점을 번호로(1번 정점, 2번 정점.. ), 간선을 양 끝점의 정점의 번호로(1-3, 3-2… ) 표기하도록 하자.
그래프의 간선에는 가중치가 있을 수도 있다. 만일 특별한 언급이 없다면 모든 간선의 가중치가 1인 그래프로 간주할 수 있으며, 가중치가 존재한다면, 예를 들어 1-3 간선의 가중치가 3이라면, 1번 정점에서 3번 정점으로 가기 위해선 길이 3인 간선을 지나야 한다고 표현한다. 위의 그래프는 모든 간선의 길이가 1인 예시라고 보면 된다.
그래프의 간선에는 방향성이 있을 수도 있다. 예를 들어, 1번과 3번 정점 사이에 놓인 1-3 간선의 경우, 1->3 또는 3->1의 방향성을 가지는 것이 가능하다. 방향성 간선을 갖고 있는 그래프를 ‘유향 그래프’, 위의 그림처럼 방향성이 없는 간선만으로 이루어진 그래프를 ‘무향 그래프’ 라 한다. 간선의 방향성은 그래프에서 탐색을 진행할 때 결과를 달리할 수 있다. 예를 들어, 현재 위의 그래프에서 1번 정점에서 4번 정점까지 가면서, 간선을 최소한 거치는 경로는 1->3->4로, 총 2개의 간선을 거친다. 우리는 이것을 ‘1번 정점과 4번 정점의 최단 경로는 2다’ 라고 표현한다. 하지만 만약 3번 정점과 4번 정점 사이의 간선이 4->3의 방향성을 가진다면, 1번 정점에서 4번 정점으로 가는 최단 경로는 1->3->6->5->4 로, 총 4개의 간선을 지나야 한다. 즉, 최단 경로가 4가 된다.
그래프에서는 ‘사이클’ 을 정의할 수 있다. 무향 그래프에서의 사이클이란, 어떤 정점에서 출발해 시작점을 제외한 어떤 정점도, 어떤 간선도 두 번 이상 방문하지 않고 시작점으로 돌아올 수 있는 경로를 의미한다. 예를 들어, 위의 그림에서는 3-6-5-4-3 사이클과, 6-7-9 사이클이 존재한다. 1-3-1은 1-3 간선을 두 번 지났으므로 사이클이 될 수 없으며, 1-3-6-5-4-3은 시작점으로 돌아오지 않는 경로이므로 사이클이 아니다.
만일 그래프에 단 하나의 사이클도 없다면, 해당 그래프는 ‘트리’ 라고 부른다. 이는 그래프가 마치 하나의 정점에서 출발해 피어난 나무 모양과도 같음에 붙여진 이름으로, 예를 들어 위의 그림에서 빨간 간선 두 개를 제거한다면 위의 그래프는 트리가 된다. 예를 들어, 상단에 주어진 그래프에서 빨간 간선 두 개를 제거한 뒤 만들어진 트리의 모습은 아래와 같다.
일반적으로 그래프에서는 정점의 위치나 간선의 모양 등에 대한 조건은 전혀 고려하지 않으며, 오직 연결성만을 고려하므로, 간선의 집합이 변하지 않는다는 가정 하에 그래프를 얼마든지 다시 그릴 수가 있다. 위의 트리에서 5번 정점을 잡고 위로 들어올리는 예시를 생각해 보자. 아래쪽에 중력이 작용한다고 생각하고 5번 정점을 위쪽으로 들어올리게 되면 트리의 모양은 아래와 같이 변할 것이다.

간선의 집합에 변함이 없는 한, 그래프는 얼마든지 원하는 대로 다시 그릴 수가 있다. 예를 들어, 위의 트리를 거울에 비추어 좌우를 바꿀 경우에도 동일한 트리가 된다.
트리에는 루트(root)가 있을 수도 없을 수도 있지만, 편의를 위해서라면 아무 정점이나 루트로 선택할 수 있다. 5번 정점을 루트로 하였다고 생각한 뒤 위의 트리를 다시 보도록 하자.
트리는 항상 루트를 기준으로 다시 그릴 수 있기 때문에, 루트가 고정되지 않는 한 어떤 정점이 ‘위에’ 있는지 판정할 수는 없다. 하지만 루트가 고정된다면, 우리는 정점 간에 ‘부모’ 와 ‘자식’ 의 관계를 정의할 수가 있다. 예를 들어, 위의 트리에서는 4번 정점의 부모는 5번 정점이며, 3번 정점은 4번 정점의 자식이 된다. 5번 정점의 부모는 없으며, 4, 6번 정점을 두 자식으로 갖게 될 것이다.
트리에는 몇 가지 중요한 성질이 있는데, 그 중 두 가지만 추려보자면 아래와 같다.
- 임의의 두 정점 U와 V에 대해, U에서 V로 가는 최단경로는 유일하다.
- 아무 정점이나 잡고 부모와의 연결을 끊었을 때, 해당 정점과 그 자식들, 그 자식들의 자식들… 로 이루어진 부분그래프는 트리가 된다.
둘 모두 직관적이며 자명한 사실이므로 증명은 생략한다. 두 번째 성질에서, 끊어진 부분그래프로 만들어진 트리를 ‘서브트리’ 라고 부른다.
만약 트리에 대한 문제 하나가 출제되었다고 가정해보자. 입력이 위처럼 루트와 그 자식들로 이루어진다면 좋지만, 루트가 없는 일반 트리의 형태(두 번째 그림)의 형태로 입력이 주어질 수도 있다. 예를 들어, 정점의 개수와 간선의 목록만이 주어진다면, 어떻게 트리를 구성할 수 있을까?
예를 들어, 위의 트리에 대해 정점의 개수와 간선의 목록이 아래와 같이 입력된다고 하자.
9
1 3
4 3
5 4
5 6
6 7
2 3
9 6
6 8
첫 줄의 9는 정점의 개수이며, 나머지 8쌍의 두 정수는 간선의 양 끝점 번호를 의미한다. 트리에서의 간선의 개수는 항상 정점의 수 - 1이라는 것은 익히 알려진 사실이며, 증명 또한 어렵지 않으므로 설명을 생략한다.
위와 같은 데이터를 트리로 구성하기 위해서는, 우선 루트 하나를 임의로 정의하는 것이 편하다. 5번 정점을 루트로 정해보도록 하자.
트리에는 부모와 자식 관계가 있으므로, 각 정점별로 부모가 누구인지, 자식들의 목록은 어떻게 되는지를 저장해 두면 요긴하게 쓰일 것이다. 이를 아래와 같이 구현할 수 있다.
def makeTree(currentNode, parent) :
for(Node in connect[currentNode]) :
if Node != parent:
add Node to currentNode’s child
set Node’s parent to currentNode
makeTree(Node, currentNode)
currentNode는 현재 탐색 중인 정점이며, parent는 해당 정점의 부모 정점이다.
트리에서는 (눈치챘을 수도 있지만) 어떤 정점의 부모는 하나이거나 없다. 따라서, 어떤 정점에 대해 연결된 모든 정점은 최대 한 개의 정점을 제외하면 모두 해당 정점의 자식들이 될 것이다. 이에 따라, 부모 정점의 정보를 가져가면서, 부모 정점이 아니면서 자신과 연결되어 있는 모든 정점을 자신의 자식으로, 자신의 자식이 될 정점들의 부모 정점을 자신으로 연결한 뒤 재귀적으로 자식 정점들에게 트리 구성을 요청하는 형태의 함수이다.
위와 같이 정의한 뒤엔, 메인 함수에서 한 차례 makeTree(5, -1) 을 호출할 경우 5번 정점을 루트로 하는 트리를 구성할 수 있다. -1은 부모가 없음을 의미한다.
그렇다면, 일반적인 형태의 트리에서 루트가 주어진 뒤 여러 질의가 주어지는 상황을 생각해 보자. 예를 들어, 5번 정점을 루트로 하는 트리에 대해, ‘정점 U를 루트로 하는 서브트리의 정점의 수는 얼마인가?’ 라는 질의가 다수 주어진다고 해 보자. U를 루트로 하는 서브트리란, 위에도 언급하였지만 정점 U와 그 부모의 연결을 끊고 정점 U를 기준으로 그 자식들, 자식들의 자식들… 로 만든 트리를 말한다. 예를 들어, 5번 정점이 루트일 때 4번 정점을 루트로 하는 서브트리에서의 정점의 수는 4개이며, 8번 정점을 루트로 하는 서브트리에서의 정점의 수는 1개가 된다.
물론 직접 연결을 끊은 뒤 다시 정점의 수를 세는 방법도 가능하겠지만, 트리의 정점 수가 많고, 질의 또한 많다면 프로그램이 제한시간 내에 수행될 수 없을 확률이 높다. 아마 미리 모든 정점을 각각 루트로 하는 서브트리에서의 정점의 수를 빠르게 구해 둘 방법이 있다면 좋을 것이다.
이를 구현하기 위해, 트리를 구성하던 코드의 동작 과정을 살펴보도록 하자. 루트에서 출발하여, 자식 정점들에 대해 한 번씩 트리 구성을 요청하게 된다. 여기에서 알 수 있는 사실은, 자식 정점들에 대한 makeTree가 호출된 뒤엔, 해당 자식 정점을 서브트리로 하는 트리가 구성이 완료된다는 것이다. 이와 같은 원리로 모든 정점에 대해 해당 정점을 루트로 하는 서브트리에 속한 정점의 수를 계산하는 함수를 만들어보도록 하자.
def countSubtreeNodes(currentNode) :
size[currentNode] = 1 // 자신도 자신을 루트로 하는 서브트리에 포함되므로 0이 아닌 1에서 시작한다.
for Node in currentNode’s child:
countSubtreeNode(Node)
size[currentNode] += size[Node]
자식 정점들에 대해 모두 서브트리에 속한 정점의 수를 계산하게 만든 뒤 각각의 정점 수를 더해 자신을 루트로 하는 서브트리에 속한 정점의 수를 만들게 된다. 이제 메인 함수 내에서 makeTree(5, -1)과 countSubtreeNodes(5) 를 차례대로 한 번씩 호출할 경우, 5번을 루트로 하는 트리에서 모든 정점에 대해 각 정점을 루트로 하는 서브트리에 속한 정점의 수를 계산해둘 수가 있다. 이를 이용하면, 모든 질의 U에 대해 size[U] 를 출력하기만 하면 되므로, 정점이 10만 개, 질의가 10만 개인 데이터에서도 충분히 빠른 시간 내에 모든 질의를 처리할 수가 있게 될 것이다.
알고리즘 분류
풀이
트리 문제이다.
트리를 순회하기 위한 dfs와, dp도 필요하다.
쿼리가 하나만 주어진다면 dp는 필요 없지만 쿼리가 여러 개이기 때문에 dp도 사용해야 한다.
우선 문제에서 루트 번호를 지정해 주는데 이를 보지 못해서 예제의 답이 이해가 되질 않았었다.
그래서 저 겁나 긴 힌트를 다 읽고 다시 위로 올라와서 루트 번호가 지정되어 있는 것을 보고 아...
항상 말하지만 문제를 잘 읽자.
무튼 문제 풀이는 다음과 같다.
우선 주어지는 트리는 항상 올바른 트리임이 보장된다고 한다. 즉, 사이클이 존재하지 않는다.
여기서 루트 노드를 지정해주니, 우리는 루트 노드에서 시작해서 모든 정점에 대해, 해당 노드에서 시작하는 서브 쿼리의 정점의 개수를 구해놓고, 쿼리마다 그 값을 가져다 출력하면 된다.
한 마디로 그냥 쿼리에서 주어지는 U를 포함한 자식 노드들의 합을 출력하면 된다.
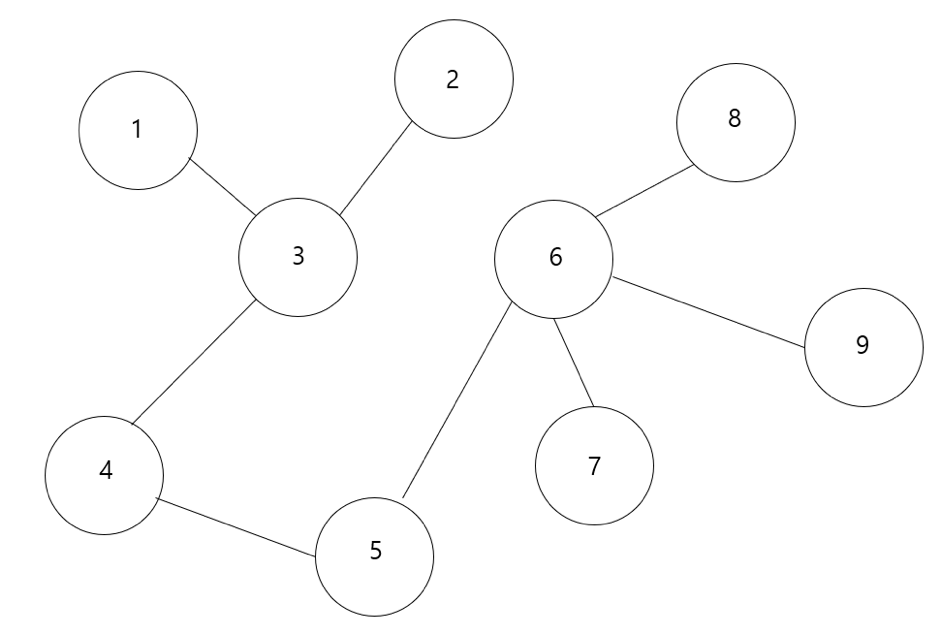
음... 그림을 그릴까 잠시 고민했지만 그냥 있는 그림을 갖다 쓰자.

입력으로 주어진 트리가 딱 이 모양이다.
여기서 루트 노드 5에서 dfs로 모든 노드를 탐색하며 서브 트리를 구할 것이다.
각 노드에서 시작된 서브트리에 포함된 정점의 개수는 subTree[]에 저장한다.
우선 5와 연결된 자식 노드 4,6으로 이동
5-> 4, 6
깊이 우선 탐색인 dfs의 다음 순서는 4의 자식 노드 방문이다.
4 -> 3
3 -> 1, 2
감이 좋거나 경험이 있는 사람은 이미 여기서 어떻게 해야 할 지 다 알고 있을 것이다.
1번 노드는 자기 자신밖에 없으니 subTree[1] = 1
2번 노드도 자기 자신밖에 없으니 subTree[2] = 1
3번 노드는 자식으로 1,2번 노드를 가지고 있는데 이 둘의 합은 2이다. 여기에 본인까지 더하면
subTree[3] = subTree[1] + subTree[2] + 1 = 3
4번 노드는 3번 노드를 자식으로 가지고 있다. subTree[4] = subTree[3] + 1 = 4
5번 노드는 4번 노드를 자식으로 가지고 있다. subTree[5] = subTree[4] + 1 = 5
이렇게 루트 노드 5의 왼쪽 서브 트리를 모두 확인했다.
나중에 쿼리에서 4번 노드를 루트로 하는 서브 트리의 정점의 개수를 요구한다고 하면
subTree[4]에 저장되어 있는 4를 출력하면 끝.
이제 루트 노드의 오른쪽을 탐색할 차례인데 굳이 여기까진 설명하지 않아도 될 것 같다.
오른쪽 서브 트리의 합을 최종적으로 루트 노드에 더해줘야 하는 것은 당연!
입력값과 출력, 예제 이미지를 잘 보고 이해했다면 나처럼 바보같이 힌트를 다 정독하지 않아도 된다.
코드
val br = System.`in`.bufferedReader()
//정점 n 2 10^5
//루트 r 1 N
//쿼리 q 1 1^5
lateinit var edge:Array<ArrayList<Int>>
lateinit var treeCnt: IntArray
lateinit var visited: BooleanArray
fun makeSubTreeCnt(n: Int,r: Int, q: Int){
visited[r] = true
if(edge[r].isEmpty()){
return
}
//루트에서 쭉쭉 내려가기
for(next in edge[r]){
if(visited[next]) continue
makeSubTreeCnt(n,next,q)
treeCnt[r]+=treeCnt[next]
}
}
fun main() = with(System.out.bufferedWriter()) {
//input
val (n,r,q) = br.readLine().split(' ').map{it.toInt()}
edge = Array(n+1){ArrayList<Int>()}
treeCnt = IntArray(n+1){1}
visited = BooleanArray(n+1)
for(i in 0 until n-1){
val (from, to) = br.readLine().split(' ').map{it.toInt()}
edge[from].add(to)
edge[to].add(from)
}
//solve
makeSubTreeCnt(n,r,q)
//output
for(i in 0 until q){
write("${treeCnt[br.readLine().toInt()]}\n")
}
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 17609 회문 Kotlin (투 포인터) (0) | 2022.04.03 |
|---|---|
| 백준 1174 줄어드는 수 Kotlin (백트래킹) (0) | 2022.04.02 |
| 백준 4358 생태학 Kotlin (map,트라이) (0) | 2022.03.31 |
| 백준 1935 후위 표기식2 Kotlin (스택) (0) | 2022.03.30 |
| 백준 17471 게리맨더링 Kotlin (조합+bfs) (0) | 2022.03.27 |




댓글