문제 출처 : https://www.acmicpc.net/problem/17471
17471번: 게리맨더링
선거구를 [1, 4], [2, 3, 5, 6]으로 나누면 각 선거구의 인구는 9, 8이 된다. 인구 차이는 1이고, 이 값보다 더 작은 값으로 선거구를 나눌 수는 없다.
www.acmicpc.net

문제
백준시의 시장 최백준은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 최백준은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 백준시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
백준시는 N개의 구역으로 나누어져 있고, 구역은 1번부터 N번까지 번호가 매겨져 있다. 구역을 두 개의 선거구로 나눠야 하고, 각 구역은 두 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
아래 그림은 6개의 구역이 있는 것이고, 인접한 구역은 선으로 연결되어 있다.

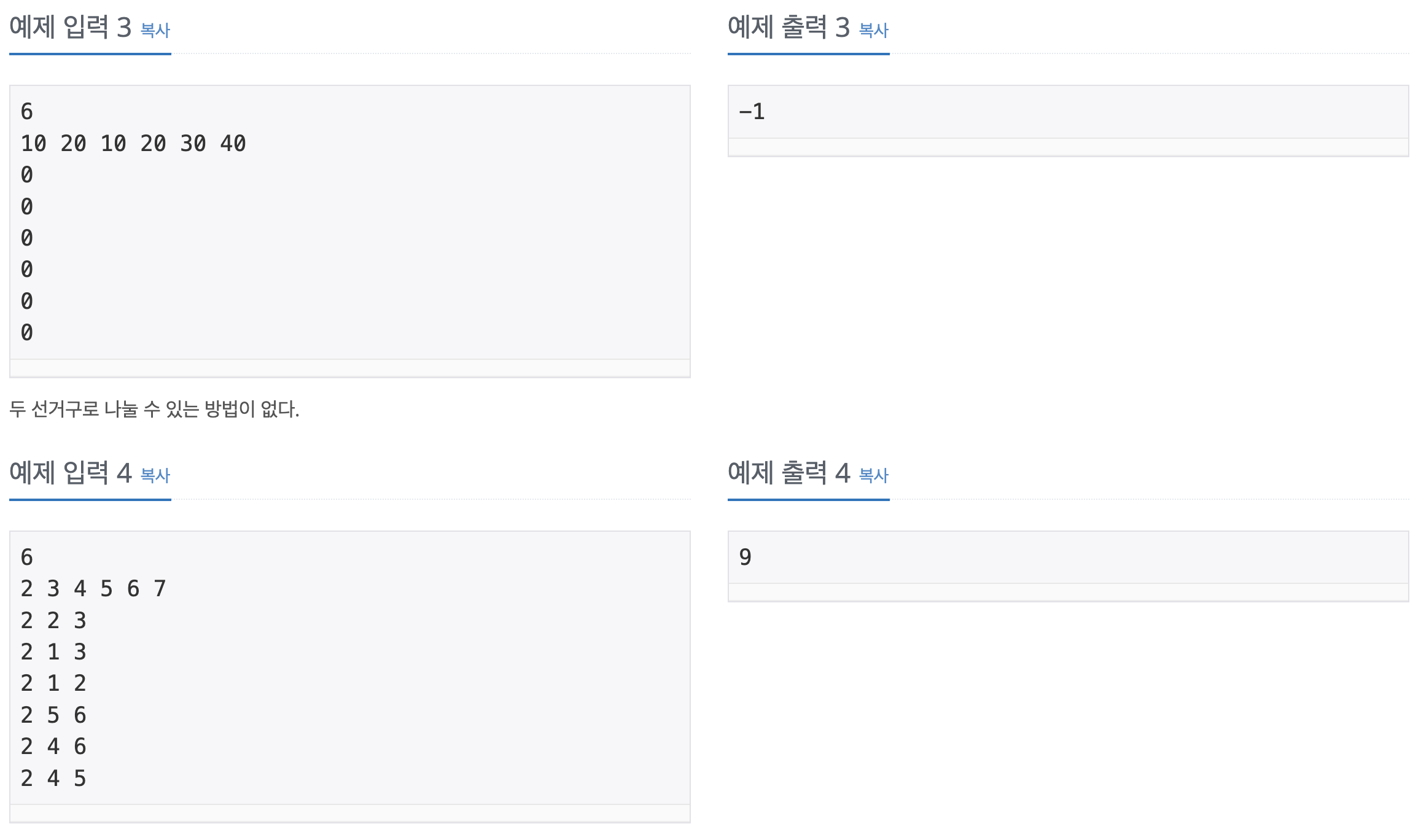
아래는 백준시를 두 선거구로 나눈 4가지 방법이며, 가능한 방법과 불가능한 방법에 대한 예시이다.

공평하게 선거구를 나누기 위해 두 선거구에 포함된 인구의 차이를 최소로 하려고 한다. 백준시의 정보가 주어졌을 때, 인구 차이의 최솟값을 구해보자.
입력
첫째 줄에 구역의 개수 N이 주어진다. 둘째 줄에 구역의 인구가 1번 구역부터 N번 구역까지 순서대로 주어진다. 인구는 공백으로 구분되어져 있다.
셋째 줄부터 N개의 줄에 각 구역과 인접한 구역의 정보가 주어진다. 각 정보의 첫 번째 정수는 그 구역과 인접한 구역의 수이고, 이후 인접한 구역의 번호가 주어진다. 모든 값은 정수로 구분되어져 있다.
구역 A가 구역 B와 인접하면 구역 B도 구역 A와 인접하다. 인접한 구역이 없을 수도 있다.
출력
첫째 줄에 백준시를 두 선거구로 나누었을 때, 두 선거구의 인구 차이의 최솟값을 출력한다. 두 선거구로 나눌 수 없는 경우에는 -1을 출력한다.
제한
- 2 ≤ N ≤ 10
- 1 ≤ 구역의 인구 수 ≤ 100

알고리즘 분류
풀이
재밌는 문제다.
그래프 관련 여러 알고리즘을 생각하고 어떤 방식으로 풀지 고민하는 과정이 재밌었던 문제.
결과적으로 대단한 풀이가 나오진 않았지만 무튼 오랜만에 해서 그런지 재밌었다.
본인은 조합 + bfs로 풀었다.
두 선거구를 나눠야 하는데, 한 선거구를 조합으로 뽑으면 나머지 노드들은 다른 한 선거구가 된다.
6개의 지역이 있을 때 1,4를 조합으로 한 선거구라고 뽑으면 2,3,5,6이 다른 선거구
1을 조합으로 한 선거구라고 뽑으면 2,3,4,5,6이 다른 선거구,
반대로 2,3,5,6을 조합으로 한 선거구라고 뽑으면 1,4가 다른 선거구가 된다.
여기서 알 수 있는 것은, 1,4를 조합으로 뽑았을 때, 2,3,5,6을 조합으로 뽑았을 때는 결국 같은 결과로, 중복이 발생된다.
따라서 N개의 지역이 있다고 할 때, N/2개만 조합으로 뽑으면 두 선거구를 선정하는 모든 경우의 수를 구할 수 있다.
정리하자면 본인의 조합+bfs 풀이에서 조합은 최대 n/2개를 뽑으며, 두 개의 선거구를 선정하는 데에 사용했다.
이제 두 선거구를 뽑았으니, 선거구A, 선거구B가 모두 연결이 되어있는지 확인해야 한다.
선거구A가 1,4
선거구B가 2,3,5,6
라고 한다면,
1,4는 연결되어있어야 하고,
2,3,5,6도 연결되어있어야 한다.
여기서 2는 3,5,6과 모두 인접할 필요는 없고, 2에서 5를 거쳐서 3을 가는 식으로 연결만 되어있으면 된다.
이를 bfs로 각 선거구의 지역들이 연결되어있는지 확인했다.
즉 조합으로 두 개의 선거구를 선정하고, bfs로 각 선거구의 지역들이 연결되어있는지 확인,
이후 두 선거구의 인구수 차이를 계산하여 최솟값으로 갱신하면 된다.
조합과 bfs를 이용하여 풀려면, 이 전체적인 틀을 벗어나지 않으면서 자기 스타일대로 구현하면 된다.
이 말은 아래 picked1, picked2를 나눈 것과, visited체크 방법, 인구수 합, 계산 방법 등을 본인 스타일대로 하면 된다는 뜻
(알고리즘 분류를 보면 알겠지만 비트마스킹을 써도 된다.)
그나저나 프로젝트 런칭 + 싸피 때문에 바빠서 요즘 문제를 풀지 못했더니 감이 다 떨어졌다.
다시 빡세게 해서 끌어올리자..
코드
import kotlin.math.abs
import java.util.*
var population = IntArray(11)
var visited = BooleanArray(11)
val edge = Array(11) { BooleanArray(11) }
var n = 0
lateinit var picked1: IntArray
val picked2 = ArrayList<Int>()
var answer = Int.MAX_VALUE
fun isConnected(picked: IntArray, len: Int, type: Int): Boolean {
val q: Queue<Int> = LinkedList()
val connectCheck = BooleanArray(11)
q.add(picked[0])
connectCheck[picked[0]] = true
while (q.isNotEmpty()) {
val cur = q.poll()
for (i in 1..n) {
//1그룹
if(type==1) {
//1그룹에 속하지 않으면 탐색 금지
if (!visited[i]) continue
}
//2그룹
else{
//2그룹에 속하지 않으면 탐색 금지
if(visited[i]) continue
}
if (edge[cur][i]) {
if (connectCheck[i]) continue
connectCheck[i] = true
q.add(i)
}
}
}
for (i in 0 until len) {
if (!connectCheck[picked[i]]) return false
}
return true
}
fun garrymend(len: Int) {
//지역구1 검사
if (!isConnected(picked1, len,1))
return
//지역구1 완성
//지역구2 검사
picked2.clear()
for (i in 1..n) {
if (visited[i]) continue
picked2.add(i)
}
if (!isConnected(picked2.toIntArray(), picked2.size,2))
return
var sum1 = 0
var sum2 = 0
for (i in 0 until len) {
sum1 += population[picked1[i]]
}
for (idx in picked2) {
sum2 += population[idx]
}
answer = answer.coerceAtMost(Math.abs(sum1 - sum2))
}
fun combination(idx: Int, len: Int) {
if (len > 0) {
garrymend(len)
}
if (len == n / 2) {
return
}
for (i in idx..n) {
picked1[len] = i
visited[i] = true
combination(i + 1, len + 1)
visited[i] = false
}
}
//2<=n<=10
fun main() = with(System.out.bufferedWriter()) {
val br = System.`in`.bufferedReader()
//input
n = br.readLine().toInt()
picked1 = IntArray(n / 2)
val tk = StringTokenizer(br.readLine())
for (i in 1..n) {
population[i] = tk.nextToken().toInt()
}
for (i in 1..n) {
val tk = StringTokenizer(br.readLine())
tk.nextToken()
while (tk.hasMoreTokens()) {
val num = tk.nextToken().toInt()
edge[i][num] = true
edge[num][i] = true
}
}
//solve
combination(1, 0)
//output
if(answer==Int.MAX_VALUE)
answer=-1
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 4358 생태학 Kotlin (map,트라이) (0) | 2022.03.31 |
|---|---|
| 백준 1935 후위 표기식2 Kotlin (스택) (0) | 2022.03.30 |
| 백준 18868 멀티버스Ⅰ Kotlin (완전탐색) (0) | 2022.03.19 |
| 백준 17427 약수의 합 2 Kotlin (에라토스테네스의 체) (0) | 2022.03.18 |
| 백준 13413 오셀로 재배치 Kotlin (그리디) (0) | 2022.03.15 |




댓글