문제 출처 : https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV5PpLlKAQ4DFAUq
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com

※ SW Expert 아카데미의 문제를 무단 복제하는 것을 금지합니다.
교도소로 이송 중이던 흉악범이 탈출하는 사건이 발생하여 수색에 나섰다.
탈주범은 탈출한 지 한 시간 뒤, 맨홀 뚜껑을 통해 지하터널의 어느 한 지점으로 들어갔으며,
지하 터널 어딘가에서 은신 중인 것으로 추정된다.
터널끼리 연결이 되어 있는 경우 이동이 가능하므로 탈주범이 있을 수 있는 위치의 개수를 계산하여야 한다.
탈주범은 시간당 1의 거리를 움직일 수 있다.
지하 터널은 총 7 종류의 터널 구조물로 구성되어 있으며 각 구조물 별 설명은 [표 1]과 같다.
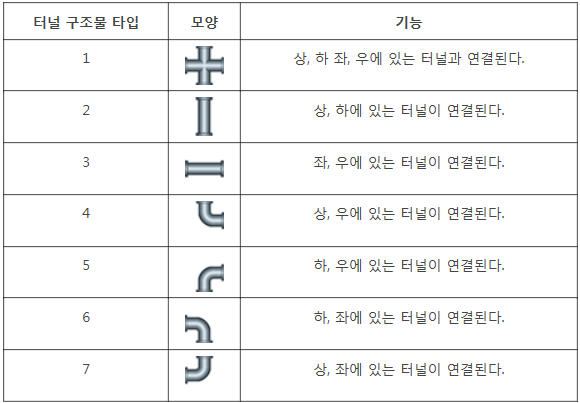
[그림 1-1] 은 지하 터널 지도의 한 예를 나타낸다.
이 경우 지도의 세로 크기는 5, 가로 크기는 6 이다.
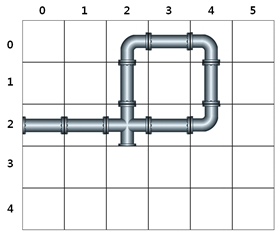
맨홀 뚜껑의 위치가 ( 2, 1 ) 으로 주어질 경우, 이는 세로 위치 2, 가로 위치 1을 의미하며 [그림 1-2] 에서 붉은 색으로 표기된 구역이다
탈주범이 탈출 한 시간 뒤 도달할 수 있는 지점은 한 곳이다.
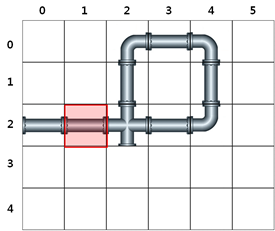
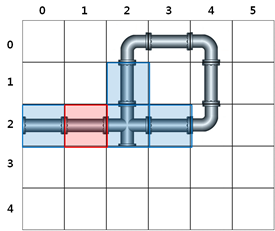
탈주범이 2시간 후 도달할 수 있는 지점은, [그림 1-3] 과 같이 맨홀 뚜껑이 위치한 붉은 색으로 표시된 지하도 와 파란색으로 표기된 지하도까지 총 3개의 장소에 있을 수 있다.
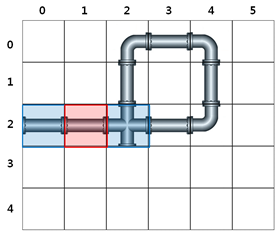
3시간 후에는 [그림 1-4] 과 같이 총 5개의 지점에 있을 수 있다.
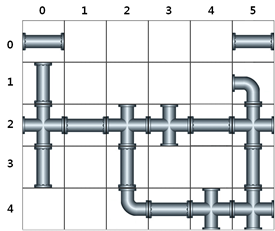
[그림 2-1] 에서 맨홀뚜껑이 위치한 지점이 ( 2, 2 ) 이고 경과한 시간이 6 으로 주어질 경우,
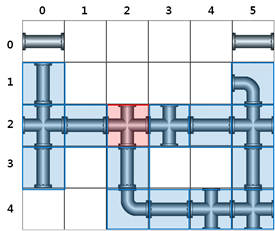
[그림 2-2] 에서 맨홀뚜껑이 위치한 지점은 붉은 색, 탈주범이 있을 수 있는 장소가 푸른색으로 표기되어 있다.
탈주범이 있을 수 있는 장소는, 맨홀뚜껑이 위치한 지점을 포함하여 총 15 개 이다.
지하 터널 지도와 맨홀 뚜껑의 위치, 경과된 시간이 주어질 때 탈주범이 위치할 수 있는 장소의 개수를 계산하는 프로그램을 작성하라.
[제약 사항]
1. 시간 제한 : 최대 50개 테이트 케이스를 모두 통과하는데, C/C++/Java 모두 1초
2. 지하 터널 지도의 세로 크기 N, 가로 크기 M은 각각 5 이상 50 이하이다. (5 ≤ N, M ≤ 50)
3. 맨홀 뚜껑의 세로 위치 R 은 0 이상 N-1이하이고 가로 위치 C 는 0 이상 M-1이하이다. (0 ≤ R ≤ N-1, 0 ≤ C ≤ M-1)
4. 탈출 후 소요된 시간 L은 1 이상 20 이하이다. (1 ≤ L ≤ 20)
5. 지하 터널 지도에는 반드시 1개 이상의 터널이 있음이 보장된다.
6. 맨홀 뚜껑은 항상 터널이 있는 위치에 존재한다.
[입력]
첫 줄에 총 테스트 케이스의 개수 T가 주어진다.
두 번째 줄부터 T개의 테스트 케이스가 차례대로 주어진다.
각 테스트 케이스의 첫 줄에는 지하 터널 지도의 세로 크기 N, 가로 크기 M, 맨홀 뚜껑이 위치한장소의 세로 위치 R, 가로 위치 C, 그리고 탈출 후 소요된 시간 L 이 주어진다.
그 다음 N 줄에는 지하 터널 지도 정보가 주어지는데, 각 줄마다 M 개의 숫자가 주어진다.
숫자 1 ~ 7은 해당 위치의 터널 구조물 타입을 의미하며 숫자 0 은 터널이 없는 장소를 의미한다.
[출력]
테스트 케이스의 개수만큼 T줄에 T개의 테스트 케이스 각각에 대한 답을 출력한다.
각 줄은 “#x”로 시작하고 공백을 하나 둔 다음 정답을 기록한다. (x는 1부터 시작하는 테스트 케이스의 번호이다)
출력해야 할 정답은 탈주범이 위치할 수 있는 장소의 개수이다.

풀이
bfs 혹은 dfs로 풀 수 있는 문제이다.
다만, 탈출된 소요 시간 L만큼의 턴(깊이)만큼만 탐색을 해야 하는데, 이는 bfs로 구현하는 것이 쉬워서 본인은 bfs로 구현하였다.
전체적인 풀이는 다음과 같다.
1. 시작점(현재 시간이 1일 때)에서 현재 시간이 L보다 작다면 다음 칸으로 이동한다.
2. 현재 칸에서 다음 칸으로 이동 가능한지 확인한다.
3. 이동 가능하다면 이동하고 visited체크, answer의 개수를 올려준다.
나이브한 풀이는 이렇고, 실제 구현하려고 하면, 터널들, 터널에 따라 다른 방향들, L만큼의 깊이만큼만 탐색 등의 문제로 고민이 많을 것인데, 이에 대한 내용들을 코드와 같이 설명하겠다.
1. 터널에 따라 다른 방향들
//상우하좌
static int[][] dir = {{-1,0},{0,1},{1,0},{0,-1}};
static int[][] haveDir = {
{},//0
{0,1,2,3},//1
{0,2},//2
{1,3},//3
{0,1},//4
{1,2},//5
{2,3},//6
{0,3}//7
};현재 문제의 그래프에서 이동 가능한 범위는 인접 4방향 (상하좌우)이다.
따라서 실제 이동 동작을 dir에 구현하고, haveDir에 각 터널 별로 상하좌우 중 어떤 방향으로 이동 가능한지 값을 저장했다.
본인은 방향 순서를 상우하좌로 잡았는데, 그냥 생각 없이 잡았다고 생각할 수 있지만 여기엔 테크닉이 들어간다.
문제에서 터널은 연결되어있어야 한다.
예를 들어 1번 터널에서 우측으로 가려면 우측에는 좌측으로 갈 수 있는 1,3,6,7 터널들이 있어야 한다.
또 4번 터널에서 위쪽으로 가려면 아래쪽으로 갈 수 있는 1,2,5,6 터널들이 있어야 한다.
이를 검사하기 위해, 상 우 하 좌를 인덱스 0,1,2,3으로 두고
0(상) -- 2(하) 방향을 매칭,
1(우) -- 3(좌) 방향을 매칭한다.
이를 매칭하는 테크닉은 현재 방향을 curDir이라 할 때 매칭할 다음 방향은 nextDir
nextDir = (curDir+2)%4 를 하면 상하,하상, 우좌,좌우 모두 매칭됨을 알 수 있다.
//다음 노드가 반대 방향 가지고 있으면 canGo == true
if(!canGo(nr,nc,(curDir+2)%4)) continue;아마 이 방향 컨트롤하는 부분을 얼마나 깔끔하게 짜느냐에 따라서 코드의 길이가 달라질 것이다.
2. L만큼의 깊이 탐색
while(!q.isEmpty()) {
int size = q.size();
for(int s =0; s<size; s++) {
Node cur = q.poll();
int curTunnel = graph[cur.r][cur.c];
for(int i=0; i<haveDir[curTunnel].length;i++) {
int curDir = haveDir[curTunnel][i];
int nr = cur.r + dir[curDir][0];
int nc = cur.c + dir[curDir][1];
if(nr<0 || nr>=n || nc<0 || nc>=m) continue;
if(graph[nr][nc]==0) continue;
//다음 노드가 반대 방향 가지고 있으면 canGo == true
if(!canGo(nr,nc,(curDir+2)%4)) continue;
if(visited[nr][nc]) continue;
visited[nr][nc] = true;
answer++;
q.add(new Node(nr,nc));
}
}
if(++time==l) return;
}기본적인 bfs의 형태는 알 것이라 생각하고, 이 코드의 핵심은
(A). int size = q.size();
(B). for(int s=0; s<size; s++)
(C). if(++time==L) return;
이다.
(A) : 에서 처음 시작점의 r,c값을 큐에 넣어놓으면 처음 size는 1이 될 것이다.
(B) : bfs는 기본적으로 큐가 계속적으로 add, pop되면서 탐색을 이어나가는데, 한 턴 한 턴 탐색을 파악할 수 없다.
이를 size로 현재 큐에 들어있는 노드들만 탐색을 진행한다는 의미이다.
(C) : 위의 size만큼의 큐 탐색이 끝나면 한 턴(한 시간)이 끝났음을 의미하기 때문에 시간을 늘려주고, L과 같은지 비교한다.
코드
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
class Node {
public int r,c;
public Node(int r, int c) {
this.r = r;
this.c = c;
}
public int getR() {
return r;
}
public int getC() {
return c;
}
}
class Solution {
static int n,m,sr,sc,l;
static int[][] graph;
static boolean[][] visited;
static int answer;
static int t;
//상우하좌
static int[][] dir = {{-1,0},{0,1},{1,0},{0,-1}};
static int[][] haveDir = {
{},//0
{0,1,2,3},//1
{0,2},//2
{1,3},//3
{0,1},//4
{1,2},//5
{2,3},//6
{0,3}//7
};
static boolean canGo(int r, int c, int direct) {
int curDir = graph[r][c];
for(int d : haveDir[curDir]) {
if(d==direct)
return true;
}
return false;
}
static void bfs() {
Queue<Node> q = new LinkedList<Node>();
q.add(new Node(sr,sc));
visited[sr][sc] = true;
int time=1;
if(time==l) return;
while(!q.isEmpty()) {
int size = q.size();
for(int s =0; s<size; s++) {
Node cur = q.poll();
int curTunnel = graph[cur.r][cur.c];
for(int i=0; i<haveDir[curTunnel].length;i++) {
int curDir = haveDir[curTunnel][i];
int nr = cur.r + dir[curDir][0];
int nc = cur.c + dir[curDir][1];
if(nr<0 || nr>=n || nc<0 || nc>=m) continue;
if(graph[nr][nc]==0) continue;
//다음 노드가 반대 방향 가지고 있으면 canGo == true
if(!canGo(nr,nc,(curDir+2)%4)) continue;
if(visited[nr][nc]) continue;
visited[nr][nc] = true;
answer++;
q.add(new Node(nr,nc));
}
}
if(++time==l) return;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(t=1; t<=T; t++) {
//input
answer=1;
StringTokenizer tk = new StringTokenizer(br.readLine());
n = Integer.parseInt(tk.nextToken());
m = Integer.parseInt(tk.nextToken());
sr = Integer.parseInt(tk.nextToken());
sc = Integer.parseInt(tk.nextToken());
l = Integer.parseInt(tk.nextToken());
graph = new int[n][m];
visited = new boolean[n][m];
for(int i=0; i<n; i++) {
tk = new StringTokenizer(br.readLine());
for(int j=0; j<m; j++) {
graph[i][j] = Integer.parseInt(tk.nextToken());
}
}
//solve
bfs();
//output
bw.write("#" + t+ " " + answer +'\n');
}
bw.close();
}
}'알고리즘 문제 풀이 > swea' 카테고리의 다른 글
| swea 5653 줄기세포 배양 Java (시뮬레이션) (0) | 2022.03.04 |
|---|---|
| swea 7465 창용 마을 무리의 개수 Java (dfs, union-find) (0) | 2022.03.03 |
| swea 2115 벌꿀채취 Java (백트래킹) (0) | 2022.03.01 |
| swea 4012 요리사 Java (조합) (0) | 2022.02.28 |
| swea 1260 화학물질2 Java (연쇄행렬 최소곱셈) (0) | 2022.02.25 |




댓글