반응형
문제 출처 : https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV5V4A46AdIDFAWu
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com

※ SW Expert 아카데미의 문제를 무단 복제하는 것을 금지합니다.
N*N 개의 벌통이 정사각형 모양으로 배치되어 있다.
각 칸의 숫자는 각각의 벌통에 있는 꿀의 양을 나타내며, 꿀의 양은 서로 다를 수 있다.
아래 [Fig. 1]은 N=4인 16개의 벌통을 나타낸다.

[Fig. 1]
각 벌통에 있는 꿀의 양이 주어졌을 때, 다음과 같은 과정으로 벌꿀을 채취하여 최대한 많은 수익을 얻으려고 한다.
① 두 명의 일꾼이 있다. 꿀을 채취할 수 있는 벌통의 수 M이 주어질 때,
각각의 일꾼은 가로로 연속되도록 M개의 벌통을 선택하고, 선택한 벌통에서 꿀을 채취할 수 있다.
단, 두 명의 일꾼이 선택한 벌통은 서로 겹치면 안 된다.
아래 [Fig. 2]는 M=2일 때, 두 일꾼이 각각 벌통을 선택하는 다양한 예를 보여준다.
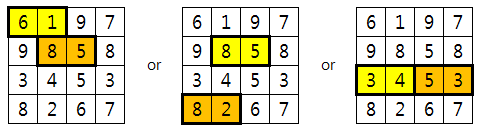
[Fig. 2]
② 두 명의 일꾼은 선택한 벌통에서 꿀을 채취하여 용기에 담아야 한다.
단, 서로 다른 벌통에서 채취한 꿀이 섞이게 되면 상품가치가 떨이지게 되므로, 하나의 벌통에서 채취한 꿀은 하나의 용기에 담아야 한다.
하나의 벌통에서 꿀을 채취할 때, 일부분만 채취할 수 없고 벌통에 있는 모든 꿀을 한번에 채취해야 한다.
두 일꾼이 채취할 수 있는 꿀의 최대 양은 C 이다.
예를 들어, 아래 [Fig. 3]에서 C=10이고, 두 명의 일꾼이 선택한 벌통이 그림과 같을 때,
첫 번째 일꾼은 꿀의 양이 6과 1인 두 개의 벌통에서 모두 꿀을 채취할 수 있다.
하지만 두 번째 일꾼은 꿀의 양이 8과 5인 두 개의 벌통에서 모두 꿀을 채취할 경우,
채취한 꿀의 양이 13이 되어 C=10을 초과하기 때문에 두 개의 벌통에서 모두 꿀을 채취할 수 없다.
따라서 두 번째 일꾼은 꿀의 양이 8과 5인 벌통 중 하나를 선택하여 꿀을 채취해야 한다.
[Fig. 3]은 그 중 한 예를 보여주고 있다.
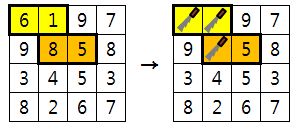
[Fig. 3]
③ 채취한 꿀은 시장에서 팔리게 된다. 이때 하나의 용기에 있는 꿀의 양이 많을수록 상품가치가 높아, 각 용기에 있는 꿀의 양의 제곱만큼의 수익이 생긴다.
예를 들어 위 [Fig. 3]과 같이 꿀을 채취할 경우, 꿀의 양이 6, 1, 8인 세 개의 용기가 얻어지며 이때 수익의 합은, (6*6) + (1*1) + (8*8) = 36 + 1 + 64 = 101 이 된다.
벌통들의 크기 N과 벌통에 있는 꿀의 양에 대한 정보, 선택할 수 있는 벌통의 개수 M, 꿀을 채취할 수 있는 최대 양 C가 주어진다.
이때 두 일꾼이 꿀을 채취하여 얻을 수 있는 수익의 합이 최대가 되는 경우를 찾고, 그 때의 최대 수익을 출력하는 프로그램을 작성하라.
[예시 1]
벌통들의 크기 N=4, 선택할 수 있는 벌통의 개수 M=2, 채취할 수 있는 꿀의 최대 양 C=13 이고,
아래 [Fig. 4]와 같이 벌통에 있는 꿀의 양의 정보가 주어진 경우를 보자.
최대 수익을 얻을 수 있는 경우 중 하나로 [Fig. 4]와 같이 벌통을 선택하여 선택하여 꿀을 채취하게 되면, 총 수익이 174가 되어 최대가 된다.
따라서 이 경우 정답은 174이다.
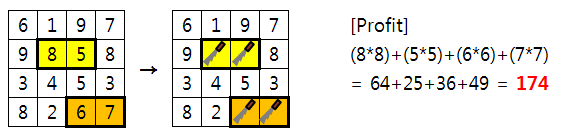
[Fig. 4]
[예시 2]
벌통의 크기 N=3, 선택할 수 있는 벌통의 개수 M=3, 채취할 수 있는 꿀의 최대 양 C=10 이고,
아래 [Fig. 5]와 같이 벌통에 있는 꿀의 양의 정보가 주어진 경우를 보자.
최대 수익을 얻을 수 있는 경우 중 하나로 [Fig. 5]와 같이 벌통을 선택하여 꿀을 채취하게 되면, 총 수익이 131이 되어 최대가 된다.
따라서 이 경우 정답은 131이다.

[Fig. 5]
[제약사항]
1. 시간제한 : 최대 50개 테스트 케이스를 모두 통과하는데, C/C++/Java 모두 3초.
2. 벌통들의 크기 N은 3 이상 10 이하의 정수이다. (3 ≤ N ≤ 10)
3. 선택할 수 있는 벌통의 개수 M은 1 이상 5 이하의 정수이다. (1 ≤ M ≤ 5)
4. 선택할 수 있는 벌통의 개수 M은 반드시 N 이하로만 주어진다.
5. 꿀을 채취할 수 있는 최대 양 C는 10 이상 30 이하의 정수이다. (10 ≤ C ≤ 30)
6. 하나의 벌통에서 채취할 수 있는 꿀의 양은 1 이상 9 이하의 정수이다.
7. 하나의 벌통에서 일부분의 꿀만 채취할 수 없고, 벌통에 있는 모든 꿀을 한번에 채취해야 한다.
[입력]
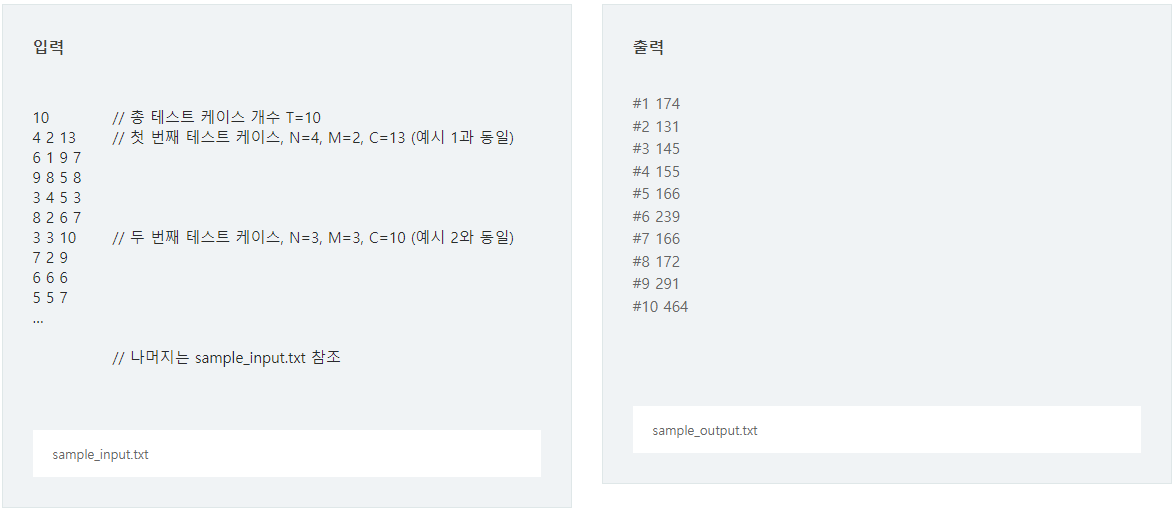
입력의 맨 첫 줄에는 총 테스트 케이스의 개수 T가 주어지고, 그 다음 줄부터 T개의 테스트 케이스가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 벌통들의 크기 N, 선택할 수 있는 벌통의 개수 M, 꿀을 채취할 수 있는 최대 양 C가 차례로 주어진다.
그 다음 줄부터 N*N 개의 벌통에서 채취할 수 있는 꿀의 양에 대한 정보가 주어진다.
[출력]
테스트 케이스의 개수만큼 T줄에 T개의 테스트 케이스 각각에 대한 답을 출력한다.
각 줄은 "#x"로 시작하고 공백을 하나 둔 다음 정답을 출력한다. (x는 1부터 시작하는 테스트 케이스의 번호이다)
출력해야 할 정답은 두 일꾼이 꿀을 채취하여 얻을 수 있는 최대 수익이다.
풀이
백트래킹, 조합, dfs에 대한 선지식이 필요하다.
전체적인 풀이는 다음과 같다.
1. 두 일꾼이 채취할 벌통을 구한다. (backtracking)
2. 두 일꾼이 채취할 벌통을 표시해 놓는다. (setSelect)
3. 두 일꾼이 채취할 벌통을 모두 뽑은 경우 두 일꾼의 벌통들에서 최대 수익을 구한다. (setMax, combination)
4. 두 일꾼이 채취한 벌통의 최대 수익 합을 갱신한다.
코드
import java.util.StringTokenizer;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
class Solution {
// 3<=n<=10
// 1<=m<=5
// 10<=c<=30
//1. 두 팀 선택 (backtracking)
//2. 팀 선택 표시 (setSelect)
//3.1 c이하 최댓값 설정 (setMax)
//3.2 c이하 최댓값 설정 (combination)
//selected[i][j] i,j번째 칸의 상태
//1 = 1팀
//2 = 2팀
static int[][] selected;
static int[][] graph;
static int N,M,C;
static int answer;
static int[] max = new int[3];
static void combination(int cnt, int r, int c, int sum, int cost) {
if(sum>C) {
return;
}
max[cnt] = Math.max(max[cnt],cost);
if(c>=N) return;
if(selected[r][c]!=cnt) return;
combination(cnt,r,c+1,sum+graph[r][c],cost + graph[r][c]*graph[r][c]);
combination(cnt,r,c+1,sum,cost);
}
static void setSelect(int cnt, int r, int c) {
for(int i=0; i<M; i++) {
//select 설정
if(selected[r][c+i]==0) {
selected[r][c+i] = cnt;
}
//select 해제
else{
selected[r][c+i] = 0;
}
}
}
static void setMax() {
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(selected[i][j]==1) {
if(max[1]!=0) continue;
combination(1,i,j,0,0);
}
else if(selected[i][j]==2) {
if(max[2]!=0) continue;
combination(2,i,j,0,0);
}
}
}
}
static void backtracking(int cnt, int idx) {
//두 팀 만들어진 경우
if(cnt==3) {
//max 초기화
max[1] = max[2] = 0;
setMax();
answer = Math.max(answer, max[1] + max[2]);
return;
}
//그래프 끝에 도착
if(idx>=N*N) return;
int r = idx/N;
int c = idx%N;
//그래프 넘어가는 경우 다음 행으로 패쓰
if(c+M>N) {
backtracking(cnt,(idx+M) - (idx+M)%N);
}
else {
//선택하고 다음 팀 고르기
setSelect(cnt,r,c);
backtracking(cnt+1,idx+M);
setSelect(cnt,r,c);
//선택하지 않고 다음 칸에서 현재 팀 고르기
backtracking(cnt,idx+1);
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(int t=1; t<=T; t++) {
//input
StringTokenizer tk = new StringTokenizer(br.readLine());
N = Integer.parseInt(tk.nextToken());
M = Integer.parseInt(tk.nextToken());
C = Integer.parseInt(tk.nextToken());
selected = new int[N][N];
graph = new int[N][N];
answer=0;
for(int i=0; i<N; i++) {
tk = new StringTokenizer(br.readLine());
for(int j=0; j<N; j++) {
graph[i][j] = Integer.parseInt(tk.nextToken());
}
}
//solve
backtracking(1,0);
//output
bw.write("#" + t+ " " + answer +'\n');
}
bw.close();
}
}반응형
'알고리즘 문제 풀이 > swea' 카테고리의 다른 글
| swea 7465 창용 마을 무리의 개수 Java (dfs, union-find) (0) | 2022.03.03 |
|---|---|
| swea 1953 탈주범 검거 Java (bfs) (0) | 2022.03.03 |
| swea 4012 요리사 Java (조합) (0) | 2022.02.28 |
| swea 1260 화학물질2 Java (연쇄행렬 최소곱셈) (0) | 2022.02.25 |
| swea 1251. [S/W 문제해결 응용] 4일차 - 하나로 Java (크루스칼) (0) | 2022.02.20 |




댓글