문제 출처 : https://www.acmicpc.net/problem/10158
10158번: 개미
가로 길이가 w이고 세로 길이가 h인 2차원 격자 공간이 있다. 이 격자는 아래 그림처럼 왼쪽 아래가 (0,0)이고 오른쪽 위가 (w,h)이다. 이 공간 안의 좌표 (p,q)에 개미 한 마리가 놓여있다. 개미는 오
www.acmicpc.net

문제
가로 길이가 w이고 세로 길이가 h인 2차원 격자 공간이 있다. 이 격자는 아래 그림처럼 왼쪽 아래가 (0,0)이고 오른쪽 위가 (w,h)이다. 이 공간 안의 좌표 (p,q)에 개미 한 마리가 놓여있다. 개미는 오른쪽 위 45도 방향으로 일정한 속력으로 움직이기 시작한다. 처음에 (p,q)에서 출발한 개미는 1시간 후에는 (p+1,q+1)로 옮겨간다. 단, 이 속력으로 움직이다가 경계면에 부딪치면 같은 속력으로 반사되어 움직인다.
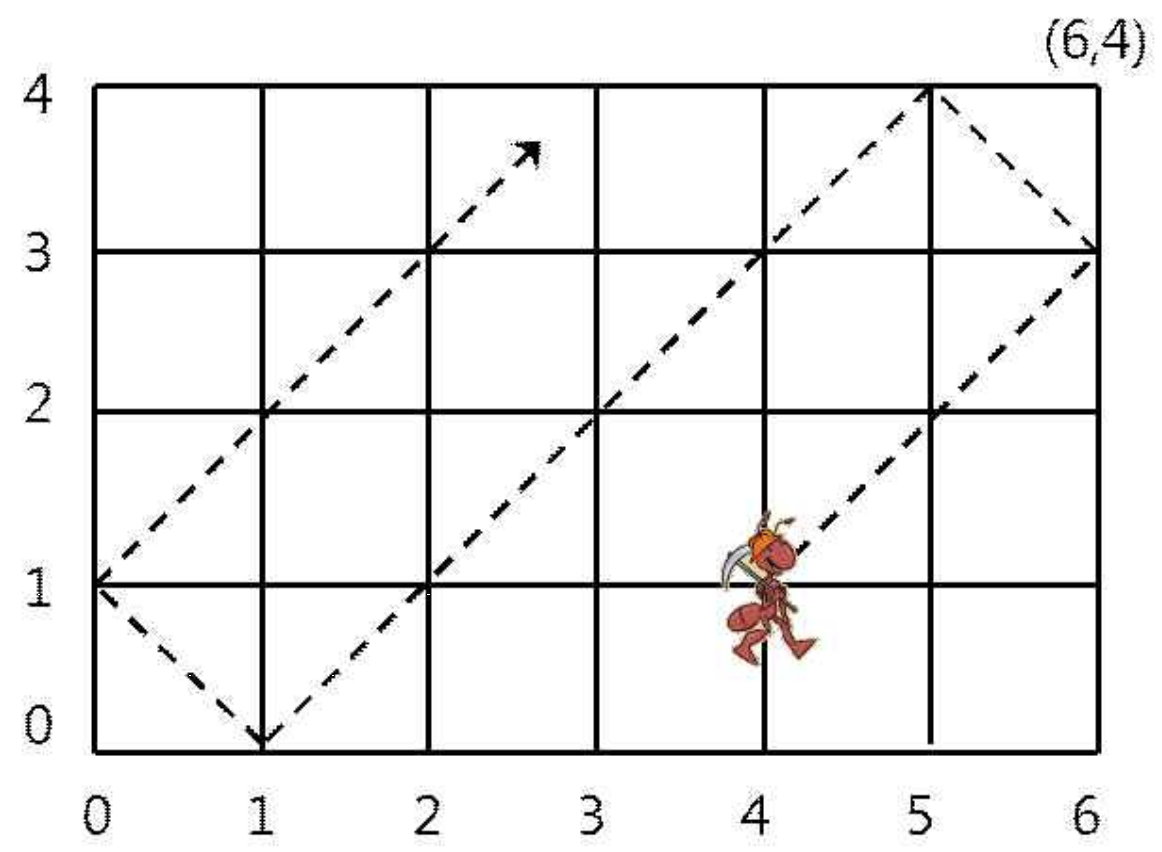
위 그림은 6×4 격자에서 처음에 (4,1)에서 출발한 개미가 움직인 길을 보여주고 있다. 처음에 (4,1)에 있는 개미는 2시간 후에 (6,3)에 있으며 8시간 후에 (0,1)에 있다. 만일 그 개미가 처음에 (5,3)에 있었다면 매 시간마다 (6,4), (5,3), (4,2), (3,1)로 움직인다.
여러분은 크기 w×h인 격자 공간에서 처음에 (p,q)에서 출발하는 개미의 t시간 후의 위치 (x,y)를 계산하여 출력해야 한다. 개미는 절대 지치지 않고 같은 속력으로 이동한다고 가정한다.
문제에서 w와 h는 자연수이며 범위는 2 ≤ w,h ≤ 40,000이다. 그리고 개미의 초기 위치 p와 q도 자연수이며 범위는 각각 0 < p < w과 0 < q < h이다. 그리고 계산할 시간 t의 범위는 1 ≤ t ≤ 200,000,000이다.
입력
첫줄에는 w와 h가 공백을 사이에 두고 주어진다. 그 다음 줄에는 초기 위치의 좌표값 p와 q가 공백을 사이에 두고 주어진다. 3번째 줄에는 개미가 움직일 시간 t가 주어진다.
출력
출력은 t 시간 후에 개미의 위치 좌표 (x,y)의 값 x와 y를 공백을 사이에 두고 출력한다.

알고리즘 분류
풀이
t가 최대 2억이기 때문에 일일이 2억 번 움직인 후의 좌표값을 구하는 것은 절대 무리이다.
게다가 빠르게 탐색한다고 해도 시간 제한이 0.15초이기 때문에 어떠한 계산을 통해 한 번에 t번만큼 이동한 후의 좌표를 구해야 함을 유추할 수 있다.
그러면 어떻게 구할 수 있을까?
p와 q의 각각 이동 경로를 보면 쉽게 떠오를 것이다.
x가 6이라고 할 때, p는 0~6을 왔다갔다,
y가 4라고 할 때, q는 0~4를 왔다갔다 하는 것을 알 수 있다.
p와 q는 어차피 x와 y의 범위 안에서만 움직이니 p와 q에 t를 더하고 x와 y로 나머지 연산을 하면 바로 구할 수 있을 것 같다! 하지만 p와 q는 단방향이 아니라 p같은 경우 좌, 우, q는 상, 하로 이동한다.
이 방향에 따라 값이 달라질 수 있기 때문에 이를 편히 구하기 위해선 격자를 두 배 크기로 늘리는 스킬이 필요하다.
가로를 예로 들면, 격자를 두 배로 늘려서 p가 0->6, 6->0로 이동하는 것을 p가 0->12로 이동하는 걸로 표현한다.
이렇게 하면 0 -> 12로 계속 단 방향으로 이동하며, 만약 현재 p의 값이 6보다 작으면 0->6방향으로 가고 있고,
p의 값이 6보다 크면 6->0(좌) 방향으로 가고 있는 것이다.
코드
import java.util.*
val br = System.`in`.bufferedReader()
fun main() = with(System.out.bufferedWriter()) {
var tk = StringTokenizer(br.readLine())
val x = tk.nextToken().toInt()
val y = tk.nextToken().toInt()
tk = StringTokenizer(br.readLine())
var p = tk.nextToken().toInt()
var q = tk.nextToken().toInt()
val t= br.readLine().toInt()
p = (t+p)%(x*2)
q = (t+q)%(y*2)
if(p>x){
p = 2*x-p
}
if(q>y){
q = 2*y-q
}
write("$p $q")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 1747 소수&팰린드롬 Kotlin (완전 탐색) (0) | 2022.02.06 |
|---|---|
| 백준 1411 비슷한 단어 Kotlin (완전 탐색) (0) | 2022.02.05 |
| 백준 2309 일곱 난쟁이 Kotlin (장풍) (0) | 2022.02.02 |
| 백준 10157 자리배정 Kotlin (구현) (0) | 2022.02.01 |
| 백준 2477 참외밭 Kotlin (기하학) (0) | 2022.01.31 |




댓글