문제 출처 : https://www.acmicpc.net/problem/2580
2580번: 스도쿠
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루
www.acmicpc.net

문제
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.
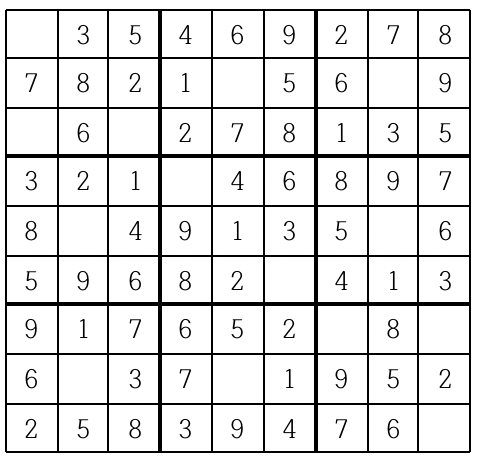
나머지 빈 칸을 채우는 방식은 다음과 같다.
- 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
- 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.

이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.

게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.
입력
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
출력
모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.
스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.
제한
- baekjoon의 백트래킹 알고리즘으로 풀 수 있는 입력만 주어진다. 다음은 그 알고리즘의 수행 시간이다.
- C++14: 80ms
- Java: 292ms
- PyPy3: 1172ms

알고리즘 분류
풀이
백트래킹 문제이다.
백트래킹은 보통 dfs에서 가지치기를 통해 탐색 가지를 줄여주는 알고리즘이다.
풀이 구상은 어렵지 않다.
0인 곳에 숫자를 a란 숫자를 넣으려면, a가 속한 가로 줄과 세로줄, 그리고 3*3 크기의 박스 내에 a란 숫자가 없어야 하며, 이는 모든 영역에 동일하게 적용되는 규칙이다.
문제에서 주어진 규칙 그대로 구현하면 된다.
0인 곳들을 찾아서, 1부터 9까지의 숫자가 가로, 세로, 박스에 있는지 검사하고 없으면 넣고 다음 0인 부분으로 넘어간다.
만약 다음 0에 숫자를 1부터 9까지 모든 숫자를 넣을 수 없는 경우, 다시 이전 0으로 돌아와서 이전 0에 다른 수를 넣어야 한다.
처음 풀 땐, dfs에 2중 for문으로 0인 부분을 만나면 1~9까지의 수를 넣을 수 있는 수를 넣고, 재귀적으로 다시 dfs 함수를 호출해 이전 행의 0열부터 다시 0인 부분을 찾아나갔다.
하지만 이땐, 0인 부분에 1~9의 숫자를 넣을 수 있는지 검사하는 함수를 unordered_set로 가로, 세로, 박스 형태에 숫자를 넣어놨더니 시간 초과.
이후, unordered_set을 사용하지 않고, 그냥 주어진 그래프에서 가로, 세로, 박스 쫘르륵 for문으로 검사하였다.
이것은 실제로 unordered_set보다 빠르게 동작하지만 또 시간 초과.
이후, 또 줄일 수 있는 부분인 dfs에서 2중 for문으로 0인 부분을 찾는 함수를 9*9 크기의 그래프에서 인덱스를 2차원으로 생각하지 않고, 0부터 81인 i에 대해 i/9는 행, i%9는 열로 하여, 우측으로 한 칸씩 넘어가며 검사하는 방식으로 바꿨다. 이는 0인 부분을 찾는 데에서 불필요한 검사를 줄여줬기 때문에 통과할 수 있었다!
아래의 코드 2,3이 위의 방식으로 푼 코드이고,
코드 1은 2차원 bool 배열을 이용해 가로, 세로, 박스 검사를 더 효율적으로 한 풀이이다.
처음 그래프를 입력받을 때, 해당 칸의 가로 줄, 세로 줄, 박스에 들어가는 숫자들을 true로 저장해두고,
dfs에서 0인 칸에 1~9를 넣을 수 있을지 검사할 때, false인 숫자만 넣을 수 있게 한 코드이다.
아래 코드에 따른 동작 시간을 보면 좋을 것 같다.
코드1(2차원 bool 배열을 이용해 가로, 세로, 박스 검사)

#include <iostream>
using namespace std;
int graph[9][9];
bool finish;
bool xSet[9][10], ySet[9][10], box[9][10];
void backTracking(int cnt) {
int r = cnt / 9;
int c = cnt % 9;
if (cnt==81) {
finish = true;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cout << graph[i][j] << ' ';
}
cout << '\n';
}
return;
}
if (graph[r][c] == 0) {
for (int k = 1; k <= 9; k++) {
if (xSet[r][k] || ySet[c][k] || box[(r / 3) * 3 + c / 3][k]) continue;
graph[r][c] = k;
xSet[r][k] = true;
ySet[c][k] = true;
box[(r / 3) * 3 + c / 3][k] = true;
backTracking(cnt+1);
if (finish) return;
graph[r][c] = 0;
xSet[r][k] = false;
ySet[c][k] = false;
box[(r / 3) * 3 + c / 3][k] = false;
}
}
else {
backTracking(cnt + 1);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cin >> graph[i][j];
xSet[i][graph[i][j]] = true;
ySet[j][graph[i][j]] = true;
box[(i / 3) * 3 + j / 3][graph[i][j]] = true;
}
}
backTracking(0);
return 0;
}코드2(주어진 graph를 이용해 가로, 세로, 박스 검사)

#include <iostream>
using namespace std;
int graph[9][9];
bool finish;
bool hasNum(int r, int c, int k) {
for (int i = 0; i < 9; i++) {
if (graph[r][i] == k) return true;
if (graph[i][c] == k) return true;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (graph[(r / 3)*3 + i][(c / 3)*3 + j] == k) return true;
}
}
return false;
}
void backTracking(int cnt) {
int r = cnt / 9;
int c = cnt % 9;
if (cnt==81) {
finish = true;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cout << graph[i][j] << ' ';
}
cout << '\n';
}
return;
}
if (graph[r][c] == 0) {
for (int k = 1; k <= 9; k++) {
if (hasNum(r, c, k)) continue;
graph[r][c] = k;
backTracking(cnt+1);
if (finish) return;
graph[r][c] = 0;
}
if ( finish) return;
}
else {
backTracking(cnt + 1);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cin >> graph[i][j];
}
}
backTracking(0);
return 0;
}코드3(unordered_set을 이용해 가로, 세로, 박스 검사)

#include <iostream>
#include <unordered_set>
using namespace std;
int graph[9][9];
unordered_set<int> xSet[9], ySet[9], boxSet[3][3];
bool finish;
void backTracking(int cnt) {
int r = cnt / 9;
int c = cnt % 9;
if (cnt==81) {
finish = true;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cout << graph[i][j] << ' ';
}
cout << '\n';
}
return;
}
if (graph[r][c] == 0) {
for (int k = 1; k <= 9; k++) {
if (xSet[r].find(k) != xSet[r].end() || ySet[c].find(k) != ySet[c].end() || boxSet[r / 3][c / 3].find(k) != boxSet[r / 3][c / 3].end()) continue;
graph[r][c] = k;
xSet[r].insert(k);
ySet[c].insert(k);
boxSet[r / 3][c / 3].insert(k);
backTracking(cnt + 1);
if (finish) return;
graph[r][c] = 0;
xSet[r].erase(k);
ySet[c].erase(k);
boxSet[r / 3][c / 3].erase(k);
}
if (finish) return;
}
else {
backTracking(cnt + 1);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cin >> graph[i][j];
xSet[i].insert(graph[i][j]);
ySet[j].insert(graph[i][j]);
boxSet[i / 3][j / 3].insert(graph[i][j]);
}
}
backTracking(0);
return 0;
}
코드4(Kotlin 2차원 Boolean 배열 이용)

import java.util.*
val br = System.`in`.bufferedReader()
//사전 순으로 앞서는 것을 출력 -> 행 박스 열 순이 유리
//위 설명 x 그냥 순서를 1부터 9까지 탐색함으로써 자동으로 사전순 정렬
val square = Array(9) { BooleanArray(10) }
val row = Array(9) { BooleanArray(10) }
val col = Array(9) { BooleanArray(10) }
var finish = false
//backtracking
fun play(idx : Int, graph : Array<IntArray>){
var idxCopy = idx
var r = 0
var c = 0
while(idxCopy<81){
r = idxCopy/9
c = idxCopy%9
if(graph[r][c]==0)
break
idxCopy++
}
if(idxCopy==81){
finish= true
return
}
for (i in 1..9) {
//해당 칸에 숫자가 들어갈 수 없으면 다음 숫자 검사
if (row[r][i]) continue
if (col[c][i]) continue
if (square[((r / 3) * 9 + c) / 3][i]) continue
//들어갈 수 있다면 넣기
graph[r][c] = i
row[r][i] = true
square[((r / 3) * 9 + c) / 3][i] = true
col[c][i] = true
//다음 0인 칸 찾기
play(idx + 1, graph)
//이전 dfs에서 종료되었다면 싹 다 return으로 종료
if (finish) return
//해당 칸에 i를 넣고 다음 0들을 검사했을 때 스도쿠가 완성될 수 없다면 다시 초기화
//return 이전에 넣으면그래프가 다시 초기화 됨에 유의
graph[r][c] = 0
row[r][i] = false
square[((r / 3) * 9 + c) / 3][i] = false
col[c][i] = false
}
}
fun main() = with(System.out.bufferedWriter()){
//input
val graph = Array(9) { r ->
val tk = StringTokenizer(br.readLine())
IntArray(9) { c ->
val num = tk.nextToken().toInt()
//row
row[r][num] = true
//col
col[c][num] = true
//square
square[((r / 3) * 9 + c) / 3][num] = true
num
}
}
//solve
play(0,graph)
//answer
for(i in 0 until 9){
for(j in 0 until 9){
write("${graph[i][j]} ")
}
write("\n")
}
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 13305 주유소 c++ (탐욕법) (0) | 2021.11.11 |
|---|---|
| 백준 2217 로프 c++ (탐욕법) (0) | 2021.11.11 |
| 백준 1053 팰린드롬 공장 c++ (dp) (0) | 2021.11.09 |
| 백준 1106 호텔 c++ (dp) (0) | 2021.11.09 |
| 백준 15483 최소 편집 c++ (dp) (0) | 2021.11.07 |




댓글