문제 출처 : https://www.acmicpc.net/problem/17485
17485번: 진우의 달 여행 (Large)
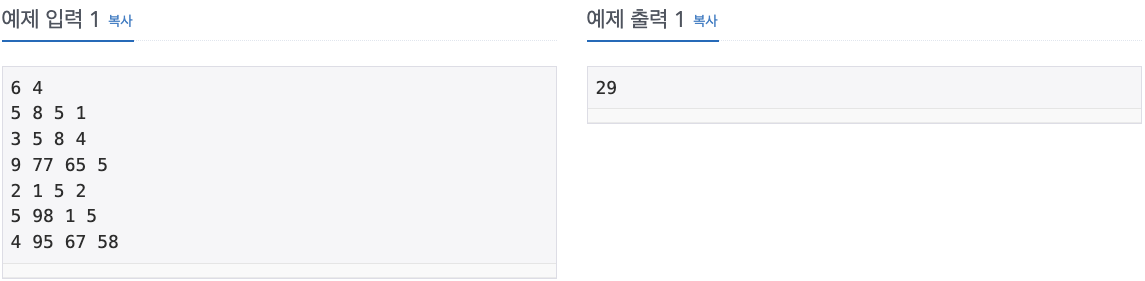
첫줄에 지구와 달 사이 공간을 나타내는 행렬의 크기를 나타내는 N, M (2 ≤ N, M ≤ 1000)이 주어진다. 다음 N줄 동안 각 행렬의 원소 값이 주어진다. 각 행렬의 원소값은 100 이하의 자연수이다.
www.acmicpc.net

문제
우주비행이 꿈이였던 진우는 음식점 '매일매일싱싱'에서 열심히 일한 결과 달 여행에 필요한 자금을 모두 마련하였다! 지구와 우주사이는 N X M 행렬로 나타낼 수 있으며 각 원소의 값은 우주선이 그 공간을 지날 때 소모되는 연료의 양이다.
[예시]

진우는 여행경비를 아끼기 위해 조금 특이한 우주선을 선택하였다. 진우가 선택한 우주선의 특징은 아래와 같다.
1. 지구 -> 달로 가는 경우 우주선이 움직일 수 있는 방향은 아래와 같다.

2. 우주선은 전에 움직인 방향으로 움직일 수 없다. 즉, 같은 방향으로 두번 연속으로 움직일 수 없다.
진우의 목표는 연료를 최대한 아끼며 지구의 어느위치에서든 출발하여 달의 어느위치든 착륙하는 것이다.
최대한 돈을 아끼고 살아서 달에 도착하고 싶은 진우를 위해 달에 도달하기 위해 필요한 연료의 최소값을 계산해 주자.
입력
첫줄에 지구와 달 사이 공간을 나타내는 행렬의 크기를 나타내는 N, M (2 ≤ N, M ≤ 1000)이 주어진다.
다음 N줄 동안 각 행렬의 원소 값이 주어진다. 각 행렬의 원소값은 100 이하의 자연수이다.
출력
달 여행에 필요한 최소 연료의 값을 출력한다.
알고리즘 분류
풀이
dp 문제이다.
처음엔 단순히 최단 경로를 찾는 다익스트라를 사용했지만 같은 방향으로 연속해서 갈 수 없다는 조건 때문에
221
818
991
위와 같은 경우 가운데 칸에 2라는 가중치가 이미 들어가 있어서 4라는 정답을 찾을 수 없게 된다.
dp로는 어떻게 풀 수 있을까?
dp[r][c][d] = r,c칸에 d방향으로 도착했을 때 최솟값
dp[r][c][0]이라고 해보자. 0은 왼쪽 대각으로 이동하는 경우이니, 0으로 r,c에 도착했다면 이전 칸은 dp[r-1][c+1][?]가 된다.
이전 칸의 방향은 0이 될 수 없으므로 1,2
즉 dp[r][c][0] = min(min(dp[r-1][c+1][1],dp[r-1][c+1][2]) + graph[r-1][c+1], dp[r][c][0])이 된다.
동일하게 1,2방향에 대해서도 위와 같은 식을 적용하고 최종적으로 마지막 라인의 최솟값을 출력하면 된다.
시간 복잡도는 O(N*M)으로 무난하게 통과할 수 있다.
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
fun getStr() = br.readLine().trim()
fun getInt() = br.readLine().trim().toInt()
lateinit var graph: Array<List<Int>>
fun main() = with(System.out.bufferedWriter()) {
//input
val (n, m) = getIntList()
graph = Array(n) { getIntList() }
val dp = Array(n + 1) { Array(m) { IntArray(3) { Int.MAX_VALUE } } }
for (c in 0 until m) {
dp[0][c].fill(0)
}
//solve
for (r in 1..n) {
for (c in 0 until m) {
if (r - 1 in 0 until n && c + 1 in 0 until m)
dp[r][c][0] = dp[r][c][0].coerceAtMost(dp[r - 1][c + 1][1].coerceAtMost(dp[r - 1][c + 1][2]) + graph[r - 1][c])
if (r - 1 in 0 until n)
dp[r][c][1] = dp[r][c][1].coerceAtMost(dp[r - 1][c][0].coerceAtMost(dp[r - 1][c][2]) + graph[r - 1][c])
if (r - 1 in 0 until n && c - 1 in 0 until m)
dp[r][c][2] = dp[r][c][2].coerceAtMost(dp[r - 1][c - 1][0].coerceAtMost(dp[r - 1][c - 1][1]) + graph[r - 1][c])
}
}
var answer = Int.MAX_VALUE
for (c in 0 until m) {
answer = answer.coerceAtMost(dp[n][c].minOrNull()!!)
}
//output
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 16202 MST 게임 Kotlin (크루스칼) (0) | 2023.04.12 |
|---|---|
| 백준 13422 도둑 Kotlin (슬라이딩 윈도우) (0) | 2023.04.11 |
| 백준 2470 두 용액 Kotlin (투 포인터) (0) | 2023.04.11 |
| 백준 2638 치즈 Kotlin (bfs) (0) | 2023.04.10 |
| 백준 2866 Kotlin 문자열 잘라내기 (이분 탐색) (0) | 2023.04.09 |




댓글