문제 출처 : https://school.programmers.co.kr/learn/courses/30/lessons/178870
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
- 연속된 부분 수열의 합
비내림차순으로 정렬된 수열이 주어질 때, 다음 조건을 만족하는 부분 수열을 찾으려고 합니다.
- 기존 수열에서 임의의 두 인덱스의 원소와 그 사이의 원소를 모두 포함하는 부분 수열이어야 합니다.
- 부분 수열의 합은 k입니다.
- 합이 k인 부분 수열이 여러 개인 경우 길이가 짧은 수열을 찾습니다.
- 길이가 짧은 수열이 여러 개인 경우 앞쪽(시작 인덱스가 작은)에 나오는 수열을 찾습니다.
수열을 나타내는 정수 배열 sequence와 부분 수열의 합을 나타내는 정수 k가 매개변수로 주어질 때, 위 조건을 만족하는 부분 수열의 시작 인덱스와 마지막 인덱스를 배열에 담아 return 하는 solution 함수를 완성해주세요. 이때 수열의 인덱스는 0부터 시작합니다.
제한사항
- 5 ≤ sequence의 길이 ≤ 1,000,000
- 1 ≤ sequence의 원소 ≤ 1,000
- sequence는 비내림차순으로 정렬되어 있습니다.
- 5 ≤ k ≤ 1,000,000,000
- k는 항상 sequence의 부분 수열로 만들 수 있는 값입니다.
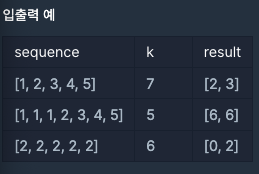
입출력 예 설명
입출력 예 #1
[1, 2, 3, 4, 5]에서 합이 7인 연속된 부분 수열은 [3, 4]뿐이므로 해당 수열의 시작 인덱스인 2와 마지막 인덱스 3을 배열에 담아 [2, 3]을 반환합니다.
입출력 예 #2
[1, 1, 1, 2, 3, 4, 5]에서 합이 5인 연속된 부분 수열은 [1, 1, 1, 2], [2, 3], [5]가 있습니다. 이 중 [5]의 길이가 제일 짧으므로 해당 수열의 시작 인덱스와 마지막 인덱스를 담은 [6, 6]을 반환합니다.
입출력 예 #3
[2, 2, 2, 2, 2]에서 합이 6인 연속된 부분 수열은 [2, 2, 2]로 3가지 경우가 있는데, 길이가 짧은 수열이 여러 개인 경우 앞쪽에 나온 수열을 찾으므로 [0, 2]를 반환합니다.
풀이
두 가지 풀이가 가능하다.
첫 번째는 투 포인터
두 번째는 이분 탐색
우선 투 포인터부터 알아보자.
핵심은 항상 K와 가깝게 sum을 유지하는 것이다.
l와 r라는 두 개의 포인터를 두고 두 포인터 사이에 값들의 합을 sum이라 정의한다.
이 sum이 k보다 크다면 R을 늘리고, sum이 k보다 크거나 같으면 L포인터를 늘린다.
R포인터를 늘린다는 것은 sum이 커지는 것을 의미하고 L포인터를 늘린다는 것은 sum이 작아진다는 것을 의미한다.
L포인터가 sequnece의 끝까지 간다면 종료되기 때문에 O(N)으로 가장 효율적인 풀이이다.
이분 탐색 풀이는 우선 우리가 몇 개의 합으로 k를 만드는지 선형 탐색한다. 이 몇 개의 합을 cnt라고 정의한다.
그럼 1부터 N까지의 cnt에 대해서 이 cnt로 k를 만드는 게 가능한지 이분 탐색한다.
이분 탐색으로 어떻게 cnt 개를 합쳐서 k를 만드는 게 가능한지 확인할 수 있을까?
우선 sequence에 대한 누적 합 배열을 만든다.
그리고 이분 탐색으로 누적 합 배열에 대해 start, end를 정의하고 mid값을 정한다.
pSum[mid + cnt] - pSum[mid] == mid에서부터 cnt개를 더한 값 (sum)
이 sum이 k보다 크거나 같다면 mid를 줄여보고 작다면 mid를 늘려본다.
k와 sum이 같은 경우 정답을 갱신하면 된다.
코드1 (투 포인터)
class Solution {
fun solution(sequence: IntArray, k: Int): IntArray {
//two pointer
var l = 0
var r = 0
var sum = sequence[r]
var answer = intArrayOf(0,Int.MAX_VALUE)
//항상 K와 가깝게
//sum이 K보다 작다면 R포인터 늘리고, sum이 k크거나 같으면 L포인터 늘리고
while(l < sequence.size){
if(sum < k){
if(r == sequence.size-1) break
sum += sequence[++r]
}else{
if(sum == k){
if(answer[1]-answer[0] > r-l){
answer[0] = l
answer[1] = r
}
}
sum -= sequence[l++]
}
}
return answer
}
}코드2 (이분 탐색)
class Solution {
fun solution(sequence: IntArray, k: Int): IntArray {
var answer: IntArray = intArrayOf()
val pSum = LongArray(sequence.size+1)
for(i in 1 .. sequence.size){
pSum[i] = pSum[i-1] + sequence[i-1]
}
//cnt로 k를 만드는 게 가능하다면 stop
for(cnt in 1 .. sequence.size){
//cnt개로 k를 만드는 데 이분 탐색하여 가장 낮은 인덱스 탐색
var left = -1
var right = -1
var s = 0
var e = sequence.size-cnt
while(s<=e){
val mid = (s+e)/2
val sum = pSum[mid+cnt] - pSum[mid]
if(sum >= k){
if(sum==k.toLong()){
left = mid
right = mid+cnt-1
}
e = mid-1
}else{
s = mid+1
}
}
if(left != -1 && right != -1) return intArrayOf(left,right)
}
return answer
}
}'알고리즘 문제 풀이 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 마법의 엘리베이터 Kotlin (그리디) (1) | 2022.12.29 |
|---|---|
| 프로그래머스 숫자 타자 대회 Kotlin (dp) (0) | 2022.12.20 |
| 프로그래머스 가장 가까운 같은 글자 Kotlin (구현) (0) | 2022.12.15 |
| 프로그래머스 할인 행사 Kotlin (Hash) (0) | 2022.12.14 |
| 프로그래머스 점 찍기 Kotlin (수학) (0) | 2022.12.11 |




댓글