문제 출처 : https://www.acmicpc.net/problem/20924
20924번: 트리의 기둥과 가지
첫 번째 줄에는 노드의 개수 $N$($1 \le N \le 200\,000$)과 루트 노드의 번호 $R$($1 \le R \le N$)이 주어진다. 이후 $N-1$개의 줄에 세 개의 정수 $a$, $b$, $d$($1 \le a, b \le N$, $ a \ne b$)가 주어진다. 이는 $a$번
www.acmicpc.net

문제
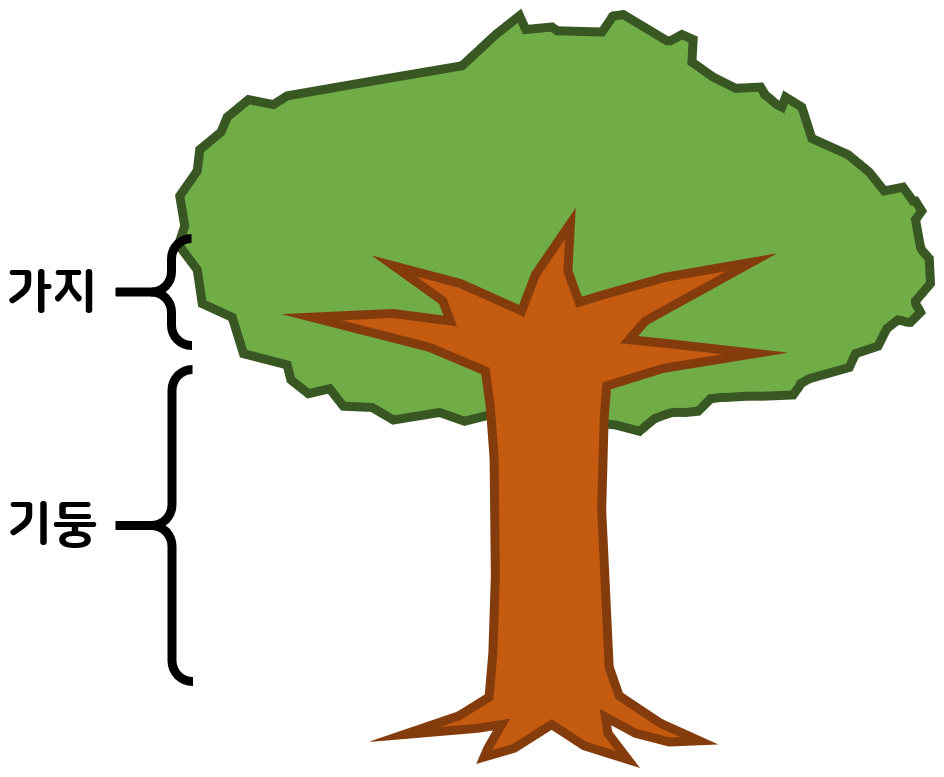
시청 공무원 마이크로는 과장으로부터 시에 있는 나무의 기둥의 길이와 가장 긴 가지의 길이를 파악하라는 업무 지시를 받았다.
마이크로는 ICPC Sinchon Winter Algorithm Camp에서 배운 트리 자료 구조를 이용하면 이 작업을 좀 더 수월하게 할 수 있으리라 판단했다.

마이크로는 트리의 기둥과 가지를 분류하기 위해 기가 노드를 추가로 정의하였다.
기가 노드는 루트 노드에서 순회를 시작했을 때, 처음으로 자식 노드가 2개 이상인 노드다. 기둥-가지를 줄여 기가 노드라 이름 붙였다. 위 그림에서 기가 노드는 4번 노드다.
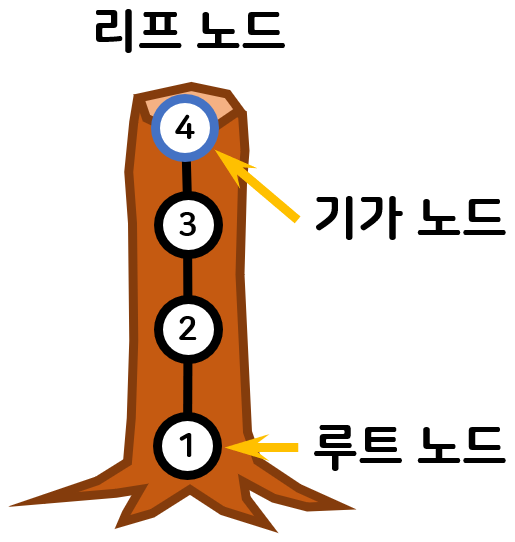
단, 위 그림과 같이 리프 노드가 단 1개인 경우 리프 노드가 동시에 기가 노드가 된다.

또한, 위 그림과 같이 루트 노드가 동시에 기가 노드인 경우도 가능하다.

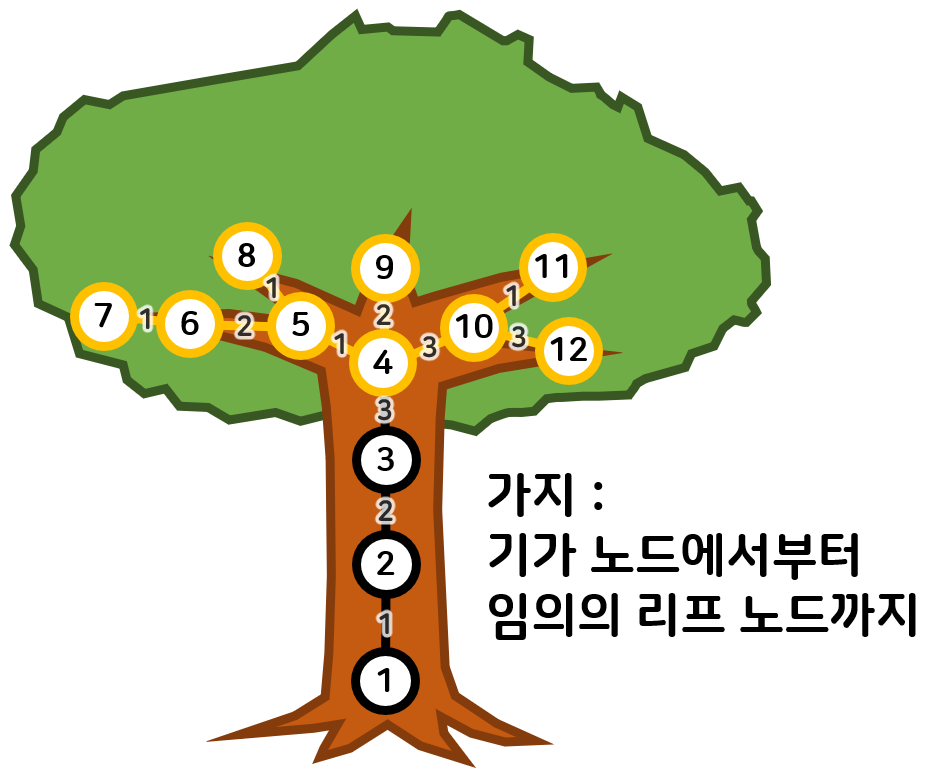
- 트리의 기둥은 루트 노드에서부터 기가 노드까지다. 위 그림에서 기둥은 1−2−3−4 이다.
기둥의 길이는 기둥의 간선 길이의 합인 1+2+3=6 이 된다. - 트리의 가지는 기가 노드에서부터 임의의 리프 노드까지다. 위 그림에서 가지는 4−5−6−7, 4−5−8, 4−9, 4−10−11, 4−10−12 총 5개가 있다.
가지의 길이는 가지의 간선 길이의 합이다. 다행히도 가장 긴 가지의 길이 하나만 기재하면 된다. 4−10−12 가지가 간선 길이의 합 3+3=6 으로 가장 긴 가지이다.
마이크로는 시의 나무를 트리 자료 구조로 옮겼다. 그런데 과장이 마이크로에게 또 다른 업무를 지시했다! 너무 바쁜 마이크로를 대신해 트리의 기둥과 가장 긴 가지의 길이를 측정하자.
입력
첫 번째 줄에는 노드의 개수 N(1≤N≤200000)과 루트 노드의 번호 R(1≤R≤N)이 주어진다.
이후 N−1개의 줄에 세 개의 정수 a, b, d(1≤a,b≤N, a≠b)가 주어진다. 이는 a번 노드와 b번 노드가 연결되어있으며 이 간선의 길이가 d(1≤d≤1000)임을 의미한다. 노드는 1번부터 N번까지 정수 번호가 매겨져 있으며 같은 간선은 여러 번 주어지지 않는다.
트리가 아닌 그래프는 입력으로 주어지지 않는다.
출력
나무의 기둥의 길이와 가장 긴 가지의 길이를 출력한다.

알고리즘 분류
풀이
트리 문제이다.
깊이 생각할 거 없다.
문제에서 주어진 대로 성실히 풀면 된다.
기둥의 길이를 출력하고, 가지의 길이중 최댓값을 출력하면 된다.
전체 트리를 탐색하면서 어디서 어디까지가 기둥이고, 어디부터 가지인지 알아야 한다.
간선의 수로 확인할 수 있을 것 같은데 이 문제는 루트가 1로 고정이 아니고 양방향 간선이다.
따라서 단순히 간선의 수로 가지를 판단하긴 어렵다. 간선이 2가지 이상인 경우..? 3가지 이상인 경우..? 양방향인데..?
따라서 본인은 outDegree라는 배열을 정의했고, 루트에서부터 dfs를 돌려서 각 노드마다 새로운 노드로 향하는 간선의 개수를 저장해 주었다.
이렇게 되면 outDegree가 2 이상인 경우엔 가지가 시작됨을 알 수 있다.
따라서 루트에서부터 탐색하면서 outDegree가 2 미만인 경우는 기둥의 길이를 더해준다.
그러다가 처음 outDegree가 2인 노드를 만나면 기둥이 끝났다는 플래그를 세워주고, 이때부턴 가지 길이를 탐색함을 의미하고, 가지의 마지막 노드에서 가지 최대 길이를 갱신해주면 된다.
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
lateinit var edge: Array<ArrayList<Pair<Int,Int>>>
var rootLen = 0
var branchLen = 0
var isRoot = true
lateinit var visited: BooleanArray
lateinit var outDegree: IntArray
fun dfs(cur: Int, dis: Int) {
var curDis = dis
visited[cur] = true
if(isRoot) rootLen = rootLen.coerceAtLeast(dis)
else branchLen = branchLen.coerceAtLeast(dis)
if(outDegree[cur] >= 2 && isRoot){
isRoot = false
curDis = 0
}
for (next in edge[cur]) {
if (visited[next.first]) continue
dfs(next.first, next.second + curDis)
}
}
fun makeDegree(cur: Int, visited: BooleanArray){
visited[cur] = true
var cnt = 0
for(next in edge[cur]){
if(visited[next.first]) continue
makeDegree(next.first,visited)
cnt++
}
outDegree[cur] = cnt
}
fun main() = with(System.out.bufferedWriter()) {
//input
val (n, root) = getIntList()
edge = Array(n+1){ ArrayList() }
visited = BooleanArray(n+1)
outDegree = IntArray(n+1)
repeat(n-1) {
val (from,to, dis) = getIntList()
edge[from].add(Pair(to,dis))
edge[to].add(Pair(from,dis))
}
//solve
makeDegree(root,BooleanArray(n+1))
dfs(root,0)
//output
write("$rootLen $branchLen")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2458 키 순서 Kotlin (플로이드 와샬) (0) | 2022.11.09 |
|---|---|
| 백준 17073 나무 위의 빗물 Kotlin (트리) (0) | 2022.11.08 |
| 백준 11585 속타는 저녁 메뉴 Kotlin (kmp) (0) | 2022.11.06 |
| 백준 1553 도미노 찾기 Kotlin (백트래킹) (0) | 2022.11.04 |
| 백준 15900 나무 탈출 Kotlin (dfs) (0) | 2022.11.03 |




댓글