문제 출처 : https://www.acmicpc.net/problem/13424
13424번: 비밀 모임
입력 데이터는 표준 입력을 사용한다. 입력은 T개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에 테스트 케이스의 개수를 나타내는 자연수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 방
www.acmicpc.net

문제
해리와 친구들은 엄브릿지의 감시를 피해 어둠의 마법 방어술을 연습하기 위한 비밀 모임을 하려고 한다. 그들은 아무도 모르게 모임의 장소를 전달하기 위해 가짜 갈레온을 사용하는데, 해리가 자신의 가짜 갈레온에 모임의 장소를 적으면 친구들이 가진 가짜 갈레온에 해리가 적은 장소가 나타난다. 해리가 다니고 있는 호그와트 마법 학교에는 모임에 사용할만한 N개의 방이 있다. 각 방에는 1부터 N까지 번호가 붙어 있으며 중복된 번호는 없다. 마법 학교답게 N개의 방은 M개의 마법으로 만들어진 비밀통로로 연결되어있다. 모든 비밀통로는 양방향 통행이 가능하며 자연수의 길이를 가진다. 모임에 참여하는 친구들은 총 K명이다.
해리는 N개의 방 중에서 한 곳을 정해 오늘 모임의 장소로 이용하려고 한다. 모임 장소를 정하기 전, 호그와트 비밀지도를 이용해 학교 안에 있는 사람들의 현재 위치를 확인해보니 모임에 참여하는 친구들은 N개의 방 중에서 한군데씩에 각각 위치해 있었다. 불행하게도 호그와트 안에서는 순간이동이 금지되어 있어서 모임에 참여하는 친구들은 들키지 않도록 비밀통로만 이용해서 오늘의 모임 장소로 가려고 한다. 이때 이들은 항상 처음 위치에서 모임 장소까지의 이동 거리가 가장 짧은 경로만을 이용한다. 여기서 ‘이동 거리’란 처음 위치에서 모임 장소까지 가기 위해 이용한 비밀 통로들의 길이의 합을 의미한다. 어느 방을 모임 장소로 사용할까 고민하던 해리는 모임에 참석하는 친구들의 이동 거리의 총합이 최소가 되는 방을 오늘의 모임 장소로 사용하기로 했다. 다음 그림은 N = 6, M = 7, K = 2인 경우의 예시이다.
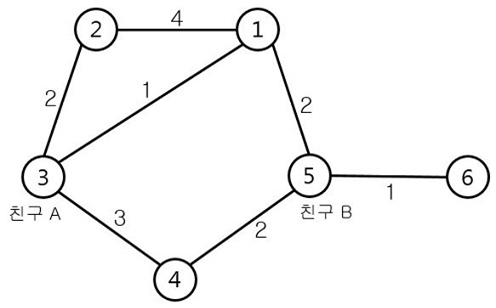
위 그래프에서 각 정점에 적힌 숫자는 방의 번호이며, 간선 위의 숫자는 방과 방을 연결하는 비밀통로의 길이이다. 모임에 참석하는 두 친구는 현재 3번, 5번 방에 있다. 만약 오늘 모임의 장소로 2번 방을 이용한다면 3번 방에 있는 친구 A의 가장 짧은 경로는 3번-2번 방 순이며 이동 거리는 2가 된다. 5번 방에 있는 친구 B의 경우 2번 방으로 가는 가장 짧은 경로는 5번-1번-3번-2번 방 순이며 이동 거리는 5가 된다. 이때, 두 친구의 이동 거리의 총합은 7이 된다. 그러나 만약 1번 방을 모임 장소로 선택한다면, 친구 A의 이동 거리는 1이 되며, 친구 B의 이동 거리는 2가 되어, 두 친구의 이동 거리의 총합은 3이 된다. 위 예시에서는 1번, 3번, 또는 5번 방을 오늘 모임의 장소로 이용했을 때 친구들의 이동 거리의 총합이 3으로 최소가 된다.
해리가 오늘의 모임 장소를 가짜 갈레온에 적으면 모임에 참여하는 K명의 친구는 그 사실을 즉시 알게 되며, 현재 하던 일을 모두 중단하고, 바로 오늘의 모임 장소로 이동한다. 해리를 위해 친구들의 이동 거리의 총합이 최소가 되도록 하는 모임 장소를 찾아 출력하는 프로그램을 작성하시오.
입력
입력 데이터는 표준 입력을 사용한다. 입력은 T개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에 테스트 케이스의 개수를 나타내는 자연수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 방의 개수 N (2 ≤ N ≤ 100), 비밀통로의 개수 M(N-1 ≤ M ≤ N(N - 1)/2)이 공백으로 구분되어 주어진다. 그 다음 줄부터 M개의 줄에 걸쳐 비밀통로의 정보(a, b, c)가 주어진다. a와 b는 비밀통로로 연결된 두 방의 번호이며 c는 a와 b를 연결하는 비밀통로의 길이이다. a와 b는 항상 다르며 c는 1 이상 1,000 이하의 자연수이다. 두 방을 연결하는 비밀통로는 반드시 하나씩만 존재한다. 또한 어떤 방에서 다른 방으로 비밀통로를 이용해서 갈 수 없는 경우는 존재하지 않으며, 같은 비밀통로에 대한 정보가 중복되어 주어지지 않는다. 비밀통로의 정보가 모두 주어진 다음 그 다음 줄에 모임에 참여하는 친구의 수 K(1 ≤ K ≤ N)가 주어진다. 각 테스트 케이스의 마지막 줄에는 모임에 참여하는 친구들이 현재 위치해 있는 방의 번호 K개가 공백으로 구분되어 주어진다. 친구들이 있는 방은 항상 N개의 방 중 하나이며, 방 번호가 중복되는 경우는 없다. 즉, 두 명 이상이 한 방에 있는 경우는 입력으로 주어지지 않는다.
출력
출력은 표준 출력을 사용한다. 입력받은 데이터에 대해, 각 테스트 케이스의 답을 순서대로 1줄에 1개씩 출력한다. 각 테스트 케이스마다 모임에 참여하는 친구들의 이동 거리의 총합이 최소가 되도록 하는 모임 장소의 방 번호를 출력한다. 만약 그러한 장소가 여러 개일 경우, 그중 번호가 가장 작은 방의 번호를 출력한다.

알고리즘 분류
풀이
플로이드 와샬 문제이다.
플로이드 와샬을 선택한 근거는, 한 좌표에서 어느 한 좌표로의 최단 거리가 아닌, 여러 좌표에서 어느 한 좌표로의 최단 거리를 알아야 하고, N이 100이기 때문에 O(N^3)의 시간 복잡도를 갖는 플로이드 와샬을 선택했다. 쓸 수만 있다면 굉장히 편하다.
플로이드 와샬의 로직은 다음과 같다.
dp[from][to] = from -> to 이동 거리
1. Array(n+1){IntArray(n+1)} 2차원 배열을 생성하고 INF값으로 초기화한다. 이때 1차원, 2차원 인덱스가 같은 경우는 0으로 초기화한다.
2. 입력 받은 간선으로 한 번에 이동 가능한 좌표들의 이동 거리를 저장한다.
3. 3중 포문을 이용해 최단 거리를 저장한다.
이렇게 플로이드 와샬로 모든 좌표에서 모든 좌표에 대한 최단 거리를 이용해서 친구들이 모임을 가질 노드를 찾는다.
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
fun getInt() = br.readLine().trim().toInt()
fun main() = with(System.out.bufferedWriter()) {
repeat(getInt()) {
val (n, m) = getIntList()
val dp = Array(n + 1) { r ->
IntArray(n + 1) { c ->
if (r == c) 0
else 987654321
}
}
repeat(m){
val (from, to, dis) = getIntList()
dp[from-1][to-1] = dis
dp[to-1][from-1] = dis
}
//floyd warshall
for(k in 0 until n){
for(i in 0 until n){
for(j in 0 until n){
dp[i][j] = dp[i][j].coerceAtMost(dp[i][k] + dp[k][j])
}
}
}
getInt()
val positions = getIntList().map{it-1}
var minSum = Int.MAX_VALUE
var answer = -1
for(to in 0 until n){
var sum = 0
for(from in positions){
sum += dp[from][to]
}
if(minSum > sum){
minSum = sum
answer = to+1
}
}
write("$answer\n")
}
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2628 종이자르기 Kotlin (정렬) (0) | 2022.09.29 |
|---|---|
| 백준 2548 대표 자연수 Kotlin (이분 탐색) (0) | 2022.09.28 |
| 백준 18223 민준이와 마산 그리고 건우 Kotlin (다익스트라) (0) | 2022.09.25 |
| 백준 17610 양팔저울 Kotlin (완전 탐색) (1) | 2022.09.22 |
| 백준 10427 빚 Kotlin (누적 합) (1) | 2022.09.21 |




댓글