문제 출처 : https://www.acmicpc.net/problem/18223
18223번: 민준이와 마산 그리고 건우
입력의 첫 번째 줄에 정점의 개수 V와 간선의 개수 E, 그리고 건우가 위치한 정점 P가 주어진다. (2 ≤ V ≤ 5,000, 1 ≤ E ≤ 10,000, 1 ≤ P ≤ V) 두 번째 줄부터 E개의 줄에 걸쳐 각 간선의 정보
www.acmicpc.net

문제
종강을 맞은 민준이는 고향인 마산으로 내려갈 계획을 짜고 있었다. 늘 그랬듯, 마산으로 갈 버스를 예약하려던 순간 민준이는 집으로 가는 다른 방법이 떠올랐다. 그것은 직접 지도를 보고 고향으로 가는 가장 짧은 길을 찾는 것이다.
그때, 먼저 고향으로 내려갔던 친구인 건우에게 연락이 왔다. 건우는 고향으로 내려가던 중 알 수 없는 일에 휘말려 외딴곳에 혼자 남겨지게 되었다. 건우는 유일한 구세주인 민준이에게 도움을 청한 것이었다. 그러나 마산의 남자인 민준이에게는 마산이 먼저였다. 민준이는 처량한 건우를 무시한 채 고향으로 떠나려고 했지만, 만약 고향으로 가는 길에 건우가 있다면 겸사겸사 도움을 줄 수 있을 것 같았다.
지도는 양방향 그래프 형태로 되어있다. 출발지는 1번 정점 마산은 V번 정점이다. 정점은 1~V까지 있다. 건우는 P번 정점에 있다.
그리고 항상 1번 정점에서 P번과 V번 정점으로 갈 수 있는 경로가 존재한다.
중복되는 간선과 자기 자신을 가리키는 간선은 존재하지 않는다.
아래와 같은 그래프가 있을 때,
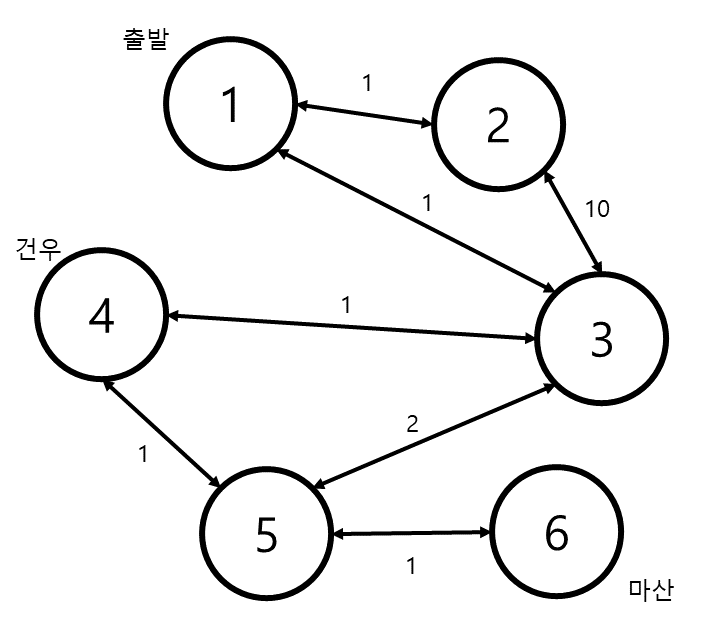
위의 경우는 최단 경로가 두 가지 있다.
1→3→4→5→6 또는 1→3→5→6 이다. 이것 중에서 건우가 있는 곳, 즉 4번 정점이 포함된 최단 경로가 있으므로 이 경우에는 민준이가 건우를 도울 수 있다.
민준이가 건우를 도와주는 경로의 길이가 최단 경로의 길이보다 길어지지 않는다면, 민준이는 반드시 건우를 도와주러 간다.
어쩌면 지킬 수도 있는 민준이의 우정을 위해 우리가 도와주자!
입력
입력의 첫 번째 줄에 정점의 개수 V와 간선의 개수 E, 그리고 건우가 위치한 정점 P가 주어진다. (2 ≤ V ≤ 5,000, 1 ≤ E ≤ 10,000, 1 ≤ P ≤ V)
두 번째 줄부터 E개의 줄에 걸쳐 각 간선의 정보 a,b,c가 공백으로 구분되어 주어진다. 이는 a번 정점과 b번 정점 사이의 거리가 c임을 의미한다. (1 ≤ a,b ≤ V, 1 ≤ c ≤ 10,000)
출력
민준이가 찾은 최단 경로 위에 건우가 있다면 "SAVE HIM" 을 아니면 "GOOD BYE" 를 출력한다.

알고리즘 분류
풀이
다익스트라 문제이다.
두 가지 풀이가 있다.
우선 핵심은 건우를 만나고 v까지 도착하는 최단거리가 이를 신경쓰지 않은 1에서 v까지 최단거리보다 크지만 않으면 된다.
건우를 만나는 것을 신경쓰지 않은 1~v 최단거리를 A
건우를 만나고 v까지 도착하는 최단 거리를 B라고 할 때,
B가 A보다 작을 일은 없지만 B<=A인 경우 건우를 구할 수 있다.
첫 번째 풀이는 다익스트라의 부등호를 조절한 풀이이다.
큐에 건우를 만났는지 안 만났는지를 가지고 다니면서, 다음 노드까지 가는 거리(X)가 이전 노드까지 온 거리 + 다음 거리 (Y)보다 작거나 같은 경우가 아닌 작은 경우만 스킵해 준다. 식으로 나타내면 다음과 같다.
dp[nextNode] < dp[currentNode] + dis
원래 다익스트라에선 dp[nextNode] <= dp[currentNode] + dis 인 경우는 거리가 같은 경우 더 탐색할 이유가 없기 때문에 <=인 경우 스킵했으나 해당 문제에선 건우를 안 만나고 이미 최단 거리를 찾았더라도 건우를 만난 경우 최단 거리를 추가로 찾아야 하기 때문이다.
<=로 한다면 위의 B인 경우를 찾지 못할 수 있다.
두 번째 풀이는 1에서 목적지까지의 최단 거리 >= 1에서 건우까지 + 건우에서 목적지까지의 최단 거리를 비교하는 것이다.
이 풀이에선 다익스트라를 두 번 돌려야하는데,
다익스트라(1~목적지)를 돌리면 1에서 건우까지, 1에서 목적지까지의 최단 거리를 구할 수 있고,
다익스트라(건우~목적지)를 돌리면 건우에서 목적지까지의 최단 거리를 구할 수 있다.
다익스트라(1~목적지)에서 구해진 건우에서 목적지까지의 거리는 최단 거리가 아닐 수 있기 때문에 다익스트라(건우~목적지)도 돌려줘야 한다.
위 내용들은 다익스트라를 잘 모르거나 이 문제를 풀기 전에 보면 잘 이해되지 않을 수 있다.
코드1
import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
fun getInt() = br.readLine().trim().toInt()
data class Node(
val num: Int,
val dis: Int,
val meet: Boolean = false
)
lateinit var edge: Array<ArrayList<Pair<Int,Int>>>
fun dijkstra(v: Int, p: Int): String{
val visited = Array(v+1){Int.MAX_VALUE}
val pq = PriorityQueue<Node>{a,b ->
a.dis-b.dis
}
pq.add(Node(1,0, p==1))
visited[1] = 0
while(pq.isNotEmpty()){
val (cNum, cDis, cMeet) = pq.poll()
if(cNum == v && cMeet) return "SAVE HIM"
if(visited[cNum] < cDis ) continue
for(i in edge[cNum].indices){
val (nNum, nDis) = edge[cNum][i]
if(visited[nNum] < cDis + nDis) continue
val nMeet = if(nNum == p) true else cMeet
visited[nNum] = cDis + nDis
pq.add(Node(nNum, cDis + nDis,nMeet))
}
}
return "GOOD BYE"
}
fun main() = with(System.out.bufferedWriter()){
//input
val (v,e,p) = getIntList()
edge = Array(v+1){ ArrayList() }
repeat(e){
val (from, to, dis) = getIntList()
edge[from].add(Pair(to,dis))
edge[to].add(Pair(from,dis))
}
//solve
write(dijkstra(v,p))
close()
}코드2
import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().trim().split(' ').map { it.toInt() }
fun getInt() = br.readLine().trim().toInt()
lateinit var edge: Array<ArrayList<Pair<Int,Int>>>
fun dijkstra(s: Int, e: Int): IntArray{
val pq = PriorityQueue<Pair<Int,Int>>{a,b -> a.second - b.second}
val dp = IntArray(e+1){Int.MAX_VALUE}
pq.add(Pair(s,0))
dp[s] = 0
while(pq.isNotEmpty()){
val (cNum,cDis) = pq.poll()
if(dp[cNum] < cDis) continue
for(next in edge[cNum]){
val (nNum, nDis) = next
if(dp[nNum] <= cDis + nDis) continue
dp[nNum] = cDis+nDis
pq.add(Pair(nNum,cDis+nDis))
}
}
return dp
}
fun main() = with(System.out.bufferedWriter()){
//input
val (v,e,p) = getIntList()
edge = Array(v+1){ ArrayList() }
repeat(e){
val (from, to, dis) = getIntList()
edge[from].add(Pair(to,dis))
edge[to].add(Pair(from,dis))
}
//solve
val dis1 = dijkstra(1,v)
val dis2 = dijkstra(p,v)
write(if(dis1[v] >= dis1[p] + dis2[v]) "SAVE HIM" else "GOOD BYE")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2548 대표 자연수 Kotlin (이분 탐색) (0) | 2022.09.28 |
|---|---|
| 백준 13424 비밀 모임 Kotlin (플로이드 와샬) (0) | 2022.09.26 |
| 백준 17610 양팔저울 Kotlin (완전 탐색) (1) | 2022.09.22 |
| 백준 10427 빚 Kotlin (누적 합) (1) | 2022.09.21 |
| 백준 1633 최고의 팀 만들기 Kotlin (dp) (1) | 2022.09.21 |




댓글