문제 출처 : https://www.acmicpc.net/problem/17780
17780번: 새로운 게임
재현이는 주변을 살펴보던 중 체스판과 말을 이용해서 새로운 게임을 만들기로 했다. 새로운 게임은 크기가 N×N인 체스판에서 진행되고, 사용하는 말의 개수는 K개이다. 말은 원판모양이고, 하
www.acmicpc.net

문제
재현이는 주변을 살펴보던 중 체스판과 말을 이용해서 새로운 게임을 만들기로 했다. 새로운 게임은 크기가 N×N인 체스판에서 진행되고, 사용하는 말의 개수는 K개이다. 말은 원판모양이고, 하나의 말 위에 다른 말을 올릴 수 있다. 체스판의 각 칸은 흰색, 빨간색, 파란색 중 하나로 색칠되어있다.
게임은 체스판 위에 말 K개를 놓고 시작한다. 말은 1번부터 K번까지 번호가 매겨져 있고, 이동 방향도 미리 정해져 있다. 이동 방향은 위, 아래, 왼쪽, 오른쪽 4가지 중 하나이다.
턴 한 번은 1번 말부터 K번 말까지 순서대로 이동시키는 것이다. 한 말이 이동할 때 위에 올려져 있는 말도 함께 이동하며, 가장 아래에 있는 말만 이동할 수 있다. 말의 이동 방향에 있는 칸에 따라서 말의 이동이 다르며 아래와 같다. 턴이 진행되던 중에 말이 4개 이상 쌓이는 순간 게임이 종료된다.
- A번 말이 이동하려는 칸이
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
- A번 말의 위에 다른 말이 있는 경우에는 A번 말과 위에 있는 모든 말이 이동한다.
- 예를 들어, A, B, C로 쌓여있고, 이동하려는 칸에 D, E가 있는 경우에는 A번 말이 이동한 후에는 D, E, A, B, C가 된다.
- 빨간색인 경우에는 이동한 후에 A번 말과 그 위에 있는 모든 말의 쌓여있는 순서를 반대로 바꾼다.
- A, B, C가 이동하고, 이동하려는 칸에 말이 없는 경우에는 C, B, A가 된다.
- A, D, F, G가 이동하고, 이동하려는 칸에 말이 E, C, B로 있는 경우에는 E, C, B, G, F, D, A가 된다.
- 파란색인 경우에는 A번 말의 이동 방향을 반대로 하고 한 칸 이동한다. 방향을 반대로 한 후에 이동하려는 칸이 파란색인 경우에는 이동하지 않고 방향만 반대로 바꾼다.
- 체스판을 벗어나는 경우에는 파란색과 같은 경우이다.
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
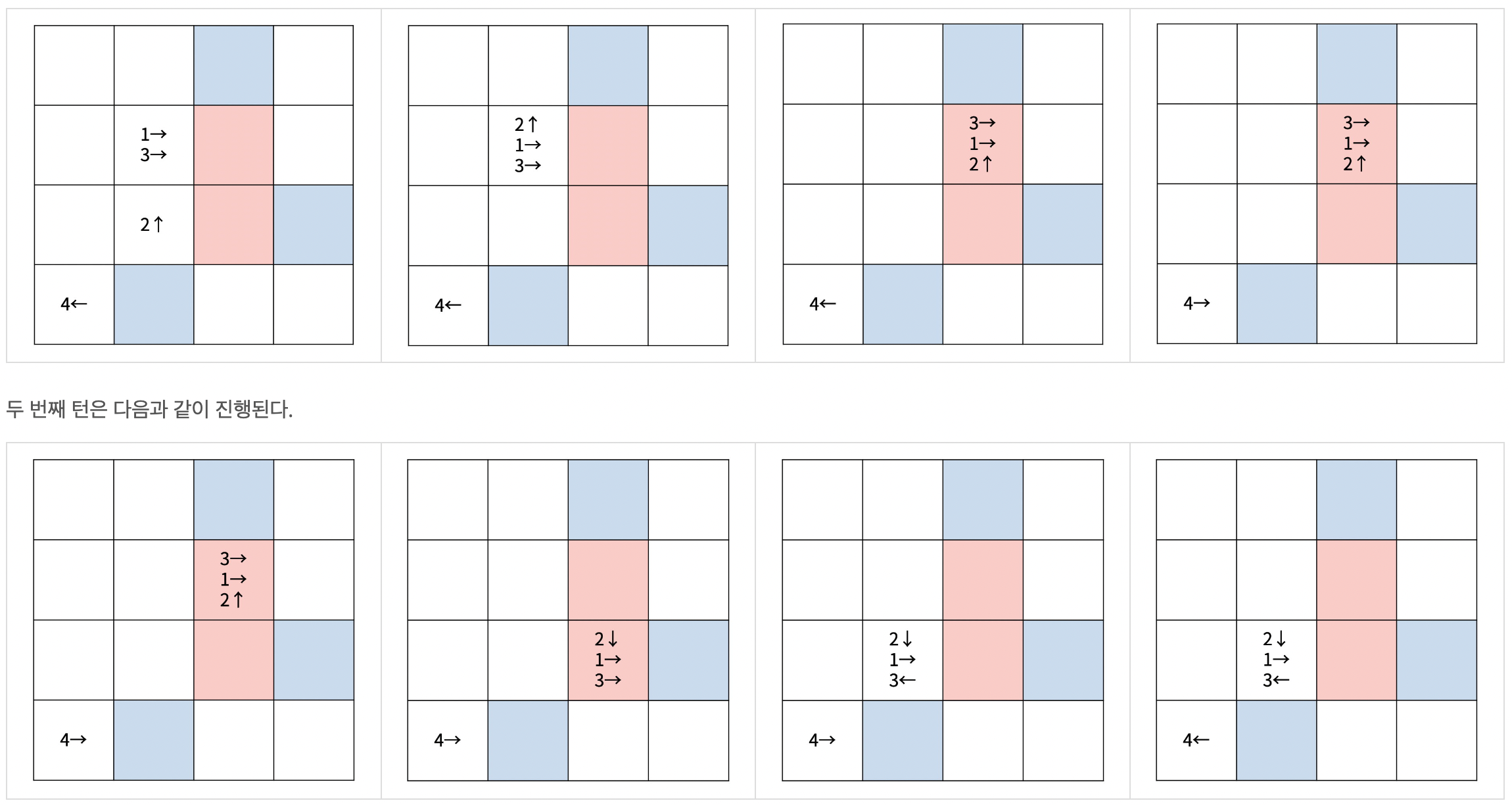
다음은 크기가 4×4인 체스판 위에 말이 4개 있는 경우이다.

첫 번째 턴은 다음과 같이 진행된다.
입력
첫째 줄에 체스판의 크기 N, 말의 개수 K가 주어진다. 둘째 줄부터 N개의 줄에 체스판의 정보가 주어진다. 체스판의 정보는 정수로 이루어져 있고, 각 정수는 칸의 색을 의미한다. 0은 흰색, 1은 빨간색, 2는 파란색이다.
다음 K개의 줄에 말의 정보가 1번 말부터 순서대로 주어진다. 말의 정보는 세 개의 정수로 이루어져 있고, 순서대로 행, 열의 번호, 이동 방향이다. 행과 열의 번호는 1부터 시작하고, 이동 방향은 4보다 작거나 같은 자연수이고 1부터 순서대로 →, ←, ↑, ↓의 의미를 갖는다.
같은 칸에 말이 두 개 이상 있는 경우는 입력으로 주어지지 않는다.
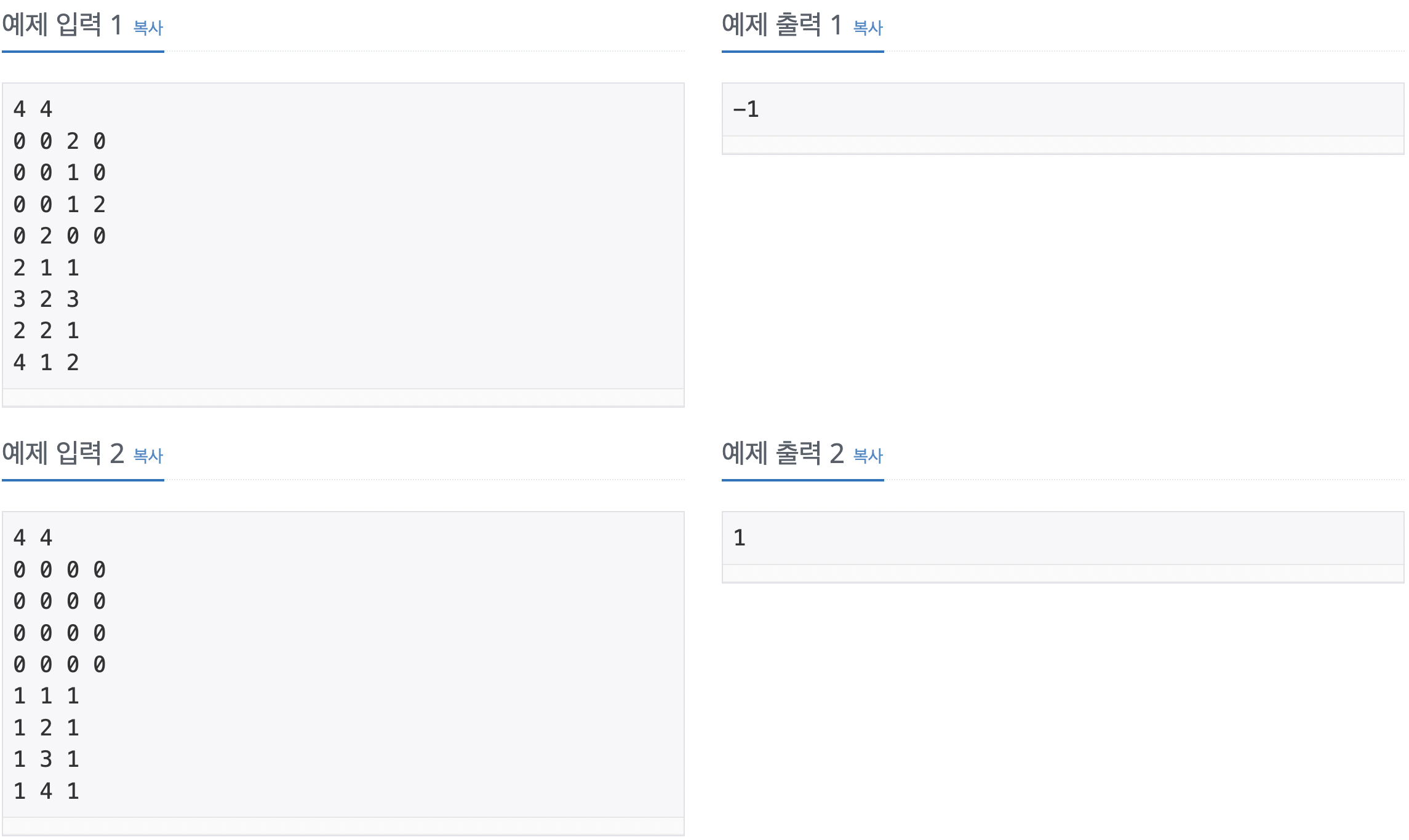
출력
게임이 종료되는 턴의 번호를 출력한다. 그 값이 1,000보다 크거나 절대로 게임이 종료되지 않는 경우에는 -1을 출력한다.
제한
- 4 ≤ N ≤ 12
- 4 ≤ K ≤ 10



알고리즘 분류
풀이
시뮬레이션 문제다.
이런 문제는 노드(여기선 말)의 상태를 어떻게 가져갈지, 이동을 어떻게 구분하고 구현할지 정의를 잘해놓아야 한다.
우선 공통 조건으로 어떤 칸에 이동했을 때 말이 있다면 그 칸의 말 위에 현재 말을 얹고, 현재 칸에 있던 말은 없애준다.
말은 여러 개가 움직일 수 있고, 가장 아래 말의 번호, 방향에 따라 움직이게 된다. 하지만 빨간색 칸을 밟는 경우 말들을 뒤집기 때문에 해당 칸에 있는 모든 말의 상태를 가지고 있어야 한다.
따라서 map[r][c] = ArrayList<Horse>로 정의할 수 있고,
Horse는 방향과 번호를 갖는다.
다음은 이동 구현이다.
이동은 빨간색 칸을 밟는 경우, 파란색 칸을 밟는 경우, 흰 칸을 밟는 경우로 나뉜다. (이동할 칸에 말이 있고 없고는 그냥 공통 조건이라 한다.)
a. 흰 칸을 밟는 경우 그냥 이동하면 된다.
b. 빨간 칸을 밟는 경우 현재 말들을 뒤집어준 다음 이동하면 된다.
파란색 칸을 밟는 경우 두 가지가 있다.
우선 방향을 바꾼다.
이때 해당 칸의 모든 말의 방향을 바꾸는 것이 아니라 맨 밑에 있는 말의 방향만 바꾼다. (따로 써져있진 않지만 문제 흐름상 그런 것 같더라..)
바꾼 상태로 다시 다음 칸을 탐색했을 때,
c. 새로운 다음 칸이 파란색 칸인 경우 움직이지 않는다. 즉, 방향만 뒤집어진 상태로 끝난다.
d. 위의 a,b 경우를 다시 체크하고 움직인다.
이렇게 4가지가 있고, 그래프를 벗어나는 경우도 파란색 칸과 동일하게 동작하므로 c,d조건에 합쳐준다.
이 문제에서 queue를 이용하면 오히려 불편한 것 같다. 그냥 맵의 좌표별로 말의 상태를 가지고 있는 게 편리하다.
이제 위 조건들을 정의했으니 풀이를 작성한다.
1. 1000번 이하 반복
2. 1~k까지 말을 순서대로 움직인다. 이때 map[0~n-1][0~n-1]을 완전탐색한다.
3. x번째 말을 찾으면 움직인다.
4. 다음 칸이 파란색인 경우 먼저 처리한다. 방향 뒤집고 이동했는데 또 다음칸이 파란색인 경우 그냥 동작을 멈추고 x+1번째 말로 넘어간다.
5. 다음 칸이 파란색인 경우는 처리됐다. 4번을 통과했다면 원래 nr,nc는 뒤집힌 방향으로 이동한 nr,nc로 초기화됐을 것이다.
6. 다음 칸이 빨간색인 경우 말들을 뒤집는다.
7. 빨간색을 뒤집은 다음은? 다음 칸이 흰 색인 경우의 동작과 같다. 이제 다음 칸에 말을 올리고, 현재 칸의 말을 없애면 된다.
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
var n = 0
var k = 0
lateinit var graph: Array<List<Int>>
//1부터k 말까지 순서대로 이동
//빨간색 이동하면 뒤집기
//파란색 이동하면 방향 반대로 바꿔서 이동
val dir = arrayOf(
//우하좌상
arrayOf(0, 1),
arrayOf(1, 0),
arrayOf(0, -1),
arrayOf(-1, 0),
)
data class Horse(
val num: Int,
var d: Int
)
lateinit var map: Array<Array<ArrayList<Horse>>>
fun simulation(): Int {
var cnt = 1
while (cnt <= 1000) {
label@ for (num in 1..k) {
for (r in 0 until n) {
for (c in 0 until n) {
//1~k중 일치하는(가장 아래에 있는 말)말이 있다면 move
if (map[r][c].isNotEmpty() && map[r][c][0].num == num) {
var curHorses = map[r][c]
var nr = r + dir[curHorses[0].d][0]
var nc = c + dir[curHorses[0].d][1]
//다음칸이 파란색이거나 바깥일 때 방향 전환
if (nr !in 0 until n || nc !in 0 until n || graph[nr][nc] == 2) {
curHorses[0].d = (curHorses[0].d + 2) % 4
nr = r + dir[curHorses[0].d][0]
nc = c + dir[curHorses[0].d][1]
//방향 전환 후 이동했을 때 또 파란색이거나 바깥일 때는 방향만 바뀌고 그대로
if (nr !in 0 until n || nc !in 0 until n || graph[nr][nc] == 2) continue@label
}
//다음 칸이 빨간색일 땐 뒤집기
if (graph[nr][nc] == 1) {
curHorses.reverse()
}
//다음 칸에 말 얹기
map[nr][nc].addAll(curHorses)
if (map[nr][nc].size >= 4) return cnt
//기존 칸 말 없애기
map[r][c].clear()
continue@label
}
}
}
}
cnt++
}
return -1
}
fun main() = with(System.out.bufferedWriter()) {
//input
getIntList().apply {
n = this[0]
k = this[1]
}
graph = Array(n) { getIntList() }
map = Array(n) { Array(n) { ArrayList() } }
//말 삽입
for (i in 1..k) {
var (r, c, d) = getIntList()
r--
c--
d = when (d) {
1 -> 0
4 -> 1
else -> d
}
map[r][c].add(Horse(i, d))
}
//solve, output
write("${simulation()}")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 1976 여행 가자 Kotlin (플로이드 와샬) (0) | 2022.07.12 |
|---|---|
| 백준 20002 사과나무 Kotlin (2차원 누적 합) (2) | 2022.07.11 |
| 백준 2346 풍선 터뜨리기 Kotlin (deque) (0) | 2022.07.10 |
| 백준 2026 소풍 Kotlin (백트래킹) (0) | 2022.07.08 |
| 백준 17779 게리맨더링 2 Kotlin (구현) (0) | 2022.07.07 |




댓글