문제 출처 : https://www.acmicpc.net/problem/9077
9077번: 지뢰제거
입력의 첫 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 10)가 주어진다. 각 테스트 케이스는 한 줄에 지뢰의 개수를 나타내는 하나의 정수 N (4 ≤ N ≤ 100,000)이 주어진 다음, N개의 좌표가 한 줄에 하
www.acmicpc.net

문제
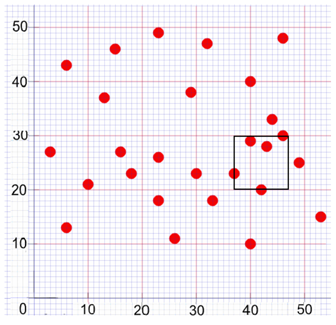
지뢰제거를 위해서 새로운 장비가 투입되었다. 이 장비를 이용하면 10m × 10m 정사각형 범위 안(경계 포함)에 있는 지뢰를 한꺼번에 제거할 수 있다. 10,000m × 10,000m의 작업장에 묻힌 지뢰의 위치를 모두 알고 있다고 할 때, 이 장치를 효과적으로 사용하기 위해서 한 번 사용하여 제거할 수 있는 최대 지뢰 개수를 계산하는 프로그램을 작성하시오. 위의 그림은 아래 "예제 입력"의 세 번째 경우를 나타낸 것이다. 그림에서 보이는 정사각형 영역에 이 장비를 사용하면 다섯 개의 지뢰를 한꺼번에 제거할 수 있으며, 이 수가 한 번 사용하여 제거할 수 있는 최대 지뢰 개수이다.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 10)가 주어진다. 각 테스트 케이스는 한 줄에 지뢰의 개수를 나타내는 하나의 정수 N (4 ≤ N ≤ 100,000)이 주어진 다음, N개의 좌표가 한 줄에 하나씩 주어진다. 각 좌표는 0이상 10,000이하의 두 정수로 주어지는데, 첫 번째 정수는 x-좌표를, 두 번째 정수는 y-좌표를 나타낸다. 모든 정수 사이에는 한 칸의 공백이 존재한다. 같은 좌표에 두 개 이상의 지뢰는 존재하지 않으며, 지뢰의 크기는 무시할 정도로 작다고 가정한다.
출력
각 테스트 케이스에 대해서 한 번에 가장 많이 제거할 수 있는 지뢰의 수를 출력한다.

알고리즘 분류
풀이
2022.05.29 - [알고리즘 문제 풀이/백준] - 백준 7573 고기잡이 Kotlin (완전 탐색)
이전 고기잡이 문제와 비슷하다.
오히려 사각형의 모양이 10*10으로 정해져 있다는 점에서 더 쉬운 문제라고 볼 수 있다.
다만 입력의 크기가 더 크다.
이 문제는 누적 합, 완전 탐색으로 풀린다.
완전 탐색의 시간 복잡도는 O(N*40*100)으로 4억이다.
테스트 케이스는 최대 10개이고 시간제한은 10초이니 한테케당 1초라고 생각하면 시간 초과가 떠야 한다고 생각했는데 통과가 되긴 한다..
40을 무시하면 1억이긴 한데 음
역시 시간 복잡도는 그저 시간 복잡도일 뿐이라 이건가
완전 극악 테케가 들어오면 시간 초과가 뜰 거 같기도 하다.
완전 탐색 풀이는 다음과 같다.
10*10크기의 사각형의 테두리는 총 가로*2 + 세로*2 총 40칸이다. 어떠한 지뢰에 대해, 이 지뢰를 이 40 칸의 테두리에 넣어서 사각형을 그리고, 그 안에 들어있는 지뢰의 수를 세어 최댓값을 구하면 된다.
정사각형의 범위 내에선, 지뢰를 항상 테두리에 걸치게 하는 것이 최선의 값을 구할 수 있다.
따라서 모든 지뢰에 대해 위의 로직을 실행하면, O(N * 40 * 100)이 된다.
// 지뢰의 수 N
// 사각형 테두리 40
// 사각형 넓이 100
만약 탐색 기준 좌표를 정사각형의 네 꼭짓점으로만 한다면 아래의 반례에 걸릴 것이다.
누적 합 풀이는 다음과 같다.
지뢰의 좌표를 입력받는 족족 해당 칸을 왼쪽 아래 꼭짓점으로 생각하고 10*10 크기의 정사각형에 모두 1만큼 더해준다.
예를 들어 3*3 크기의 정사각형이라고 해 보고, 두 개의 좌표를 받았다고 생각해 보자.
| 1 | 1 | 1 | |||
| 1 | 1 | 2 | 1 | 1 | |
| 1 | 1 | 2 | 1 | 1 | |
| 1 | 1 | 1 | |||
빨간 숫자가 입력받은 지뢰의 좌표이다.
이 경우 정답은 2가 된다.
숫자의 의미는, 어떠한 위치에서 3*3의 정사각형을 그렸을 때 숫자가 2인 칸이 정사각형 내부에 포함된다면 이 정사각형은 두 개의 지뢰를 제거할 수 있다는 의미이다.
따라서 그래프에서 가장 높은 값이 답이 된다.
코드1 (완전 탐색)

val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
lateinit var mine: Array<Pair<Int, Int>>
lateinit var graph: Array<BooleanArray>
fun main() = with(System.out.bufferedWriter()) {
val T = getInt()
for (t in 1..T) {
//input
var answer = 0
val n = getInt()
mine = Array(n) { Pair(0, 0) }
graph = Array(10000) { BooleanArray(10000) }
for (i in 0 until n) {
val (c, r) = getIntList()
mine[i] = Pair(r, c)
graph[r][c] = true
}
//solve
mine.forEach {
val (r, c) = it
//100개의 사각형 테두리 좌표를 기준으로 사각형 그려보기
for (i in 0..10) {
for (j in 0..10) {
val cr = r - i
val cc = c - j
var cnt = 0
for (a in 0..10) {
for (b in 0..10) {
val nr = cr + a
val nc = cc + b
if (nr !in 0 until 10000 || nc !in 0 until 10000) continue
if (graph[nr][nc]) cnt++
}
}
answer = answer.coerceAtLeast(cnt)
//기준은 테두리로만 자으면 됨
if(i!=0 && i!=10 ) break
}
}
}
//output
write("$answer\n")
}
close()
}코드2 (누적 합)

val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
val preSum = Array(10000){IntArray(10000)}
fun main() = with(System.out.bufferedWriter()){
repeat(getInt()){//t
var answer = 0
repeat(getInt()){//n
val (x,y) = getIntList()
//solve
for(x in x .. (x+10).coerceAtMost(9999)){
for(y in y .. (y+10).coerceAtMost(9999)){
answer = answer.coerceAtLeast(++preSum[x][y])
}
}
}
//output
write("$answer\n")
//reset
for(i in 0 until 10000){
for(j in 0 until 10000){
preSum[i][j] = 0
}
}
}
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 18818 Iguana Instructions Kotlin (bfs) (0) | 2022.06.03 |
|---|---|
| 백준 22352 항체 인식 Kotlin (dfs) (0) | 2022.06.02 |
| 백준 20444 색종이와 가위 Kotlin (이분 탐색) (0) | 2022.05.30 |
| 백준 7573 고기잡이 Kotlin (완전 탐색) (0) | 2022.05.29 |
| 백준 16946 벽 부수고 이동하기 4 Kotlin (bfs) (0) | 2022.05.28 |




댓글