문제 출처 : https://www.acmicpc.net/problem/7573
7573번: 고기잡이
한국인의 식단에서 생선은 매우 중요한 단백질 공급원이다. 반면, 지구 온난화로 인한 바닷물의 온도 상승, 그리고 지금까지 마구잡이로 물고기를 잡은 결과로 점점 우리나라의 바다에서 물고
www.acmicpc.net

문제
한국인의 식단에서 생선은 매우 중요한 단백질 공급원이다. 반면, 지구 온난화로 인한 바닷물의 온도 상승, 그리고 지금까지 마구잡이로 물고기를 잡은 결과로 점점 우리나라의 바다에서 물고기의 수가 줄어들고 있다. 정부에서는 이 문제를 심각하게 생각하여, 물고기를 잡을 수 있는 곳과 여기서 고기잡이 배가 사용할 수 있는 그물의 폭에 제한을 두었다. 물고기는 바다 표면 근처에 살기 때문에, 그물의 높이는 중요하지 않다. 따라서 그물은 길이가 l인 직선으로 생각할 수 있고, 물고기를 잡을 때, 그물은 한 변의 길이가 1 이상 정수인 직사각형 모양으로 치게 된다. 예를 들어, l = 10이라면, 칠 수 있는 그물의 모양은 1×4, 2×3, 3×2, 4×1과 같이 4가지 형태의 직사각형이 된다.
고기를 잡을 수 있는 곳은 N×N 크기의 모눈종이 모양으로 되어 있다. 각 모눈에는 좌표가 주어지며, 가장 왼쪽 위 모눈이 (1,1)이고, 가장 오른쪽 아래 모눈이 (N,N)이다. 총 M 마리의 물고기가 서로 다른 모눈 위에 한 마리씩 살고 있으며, 물고기는 움직이지 않는다. 고기잡이 배는 한 모눈 위에 위치를 잡고 자신의 오른쪽과 아래쪽으로 그물을 친다. 일단 그물을 치면, 그물 안, 그리고 그물에 걸친 물고기들을 잡을 수 있다. 예를 들면, 다음 그림은 N = 7, l = 10 이고 M = 6 마리의 물고기가 (2,2), (2,4), (3,3), (5,6), (6,2), (7,4)에 살고 있을 때, (2,2)에 놓인 고기잡이 배가 2×3 모양으로 그물을 친 예를 보이고 있다. 이때 고기잡이 배는 총 3마리의 물고기를 잡을 수 있다. 고기를 잡을 수 있는 영역 밖으로 그물을 치는 경우는 없다.
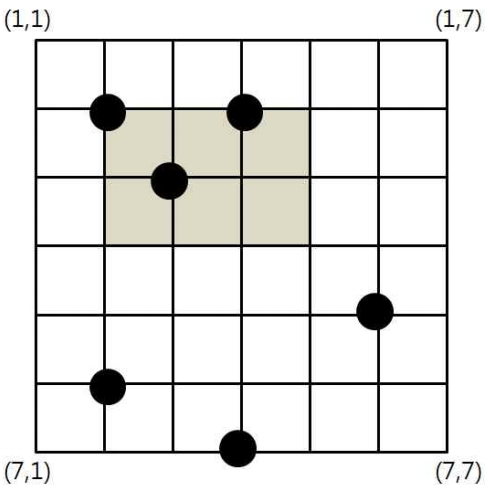
고기를 잡을 수 있는 영역, 물고기의 위치, 그물의 폭이 주어졌을 때 한 번의 그물치기로 잡을 수 있는 가장 많은 물고기의 마릿수를 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에는 모눈종이의 크기, 그물의 길이, 물고기의 수를 나타내는 세 개의 정수 N, l, M이 하나의 공백을 두고 주어진다. 단, 2 ≤ N ≤ 10,000, 4 ≤ l ≤ 100, 1 ≤ M ≤100 이다. l은 l ≤ 4N - 4을 만족하는 짝수이다. 두 번째 줄부터 이후 M 개의 줄에는 각 물고기의 좌표가 하나의 공백을 두고 주어진다. 물고기의 좌표 순서는 무작위로 주어진다.
출력
첫 줄에 주어진 입력에서 잡을 수 있는 가장 많은 물고기의 마릿수를 하나의 정수로 출력한다.
알고리즘 분류
풀이
완탐 문제이다.
그래프의 크기가 n*n이기 때문에 당연히 모든 칸에 그물을 쳐볼 수 없다.
그러면 물고기를 기준으로 탐색을 해야 하는데, 고려할 점이 두 가지가 있다.
1. (x,y) 좌표에 물고기가 있다고 할 때, 이 주변으로 그물을 쳐봐야 하는 건 알겠는데, 어디어디 쳐봐야 할까?
2. 그물의 가로와 세로는 정해져있지 않고, 길이만 정해져있다. 즉, 이 길이로 여러 직사각형 모양의 그물을 만들 수 있다.
우선, 여러 모양의 그물을 만드는 것은 쉽다.
w와 h는 2 개씩 있으니, h = l/2 -w가 된다.
l이 10일 때, w가 1이라면 h=4
w가 2라면 h=3
w가 3이라면 h=2
w가 4라면 h=1
w와 h는 l/2미만이다.
이제 위의 방법으로 여러 모양의 그물을 만들어서 어떠한 좌표에 펼쳐 가장 많은 물고기를 잡을 때의 물고기 수를 구하면 된다.
물고기를 가장 많이 포함할 수 있게 그물을 치는 방법은, 어떠한 좌표에 물고기가 있다고 하면, 그 물고기를 그물에 걸치게끔 그물을 던져보는 것이다. 즉 2*3 모양의 그물이 있다고 하면, 이 직사각형의 테두리에 물고기를 걸치게끔 그물을 던지는 것이다.
O(l/2 * m * 그물 테두리의 좌표 개수)-> O(lm) 의 시간 복잡도로 답을 찾을 수 있다.
코드
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
var answer = 0
//그물 치기
fun cast(r: Int, c: Int, l: Int, n: Int){
var w = 1
while(w*2 < l){
val h = (l - w*2)/2
//w,h로 그물 쳐보기
for(i in 0 .. h){
label@for(j in 0 .. w){
val cr = r - i
val cc = c - j
var cnt=0
for(ii in 0 .. h){
for(jj in 0 .. w){
val nr = cr + ii
val nc = cc + jj
if(nr !in 1 .. n || nc !in 1 .. n) continue@label
if(graph[nr][nc]) cnt++
}
}
answer = answer.coerceAtLeast(cnt)
if(i!=0 && i!=h ) break
}
}
w++
}
}
lateinit var graph: Array<BooleanArray>
val fish = ArrayList<Pair<Int,Int>>()
fun main() = with(System.out.bufferedWriter()){
//input
val (n,l,m) = getIntList()
graph = Array(n+1){BooleanArray(n+1)}
repeat(m){
val (r,c) = getIntList()
graph[r][c] = true
fish.add(Pair(r,c))
}
//solve
fish.forEach { (r,c) ->
cast(r,c,l,n)
}
//output
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 9077 지뢰제거 Kotlin (누적 합, 완전 탐색) (0) | 2022.05.31 |
|---|---|
| 백준 20444 색종이와 가위 Kotlin (이분 탐색) (0) | 2022.05.30 |
| 백준 16946 벽 부수고 이동하기 4 Kotlin (bfs) (0) | 2022.05.28 |
| 백준 2661 좋은수열 Kotlin (백트래킹) (0) | 2022.05.26 |
| 백준 14442 벽 부수고 이동하기 2 Kotlin (bfs) (0) | 2022.05.25 |




댓글