문제 출처 : https://programmers.co.kr/learn/courses/30/lessons/12914
코딩테스트 연습 - 멀리 뛰기
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는 (1칸, 1칸, 1칸, 1칸) (1칸, 2칸, 1칸) (1칸, 1칸, 2칸) (2칸, 1칸, 1칸) (2칸, 2
programmers.co.kr
문제 설명
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는
(1칸, 1칸, 1칸, 1칸)
(1칸, 2칸, 1칸)
(1칸, 1칸, 2칸)
(2칸, 1칸, 1칸)
(2칸, 2칸)
의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567를 나눈 나머지를 리턴하는 함수, solution을 완성하세요. 예를 들어 4가 입력된다면, 5를 return하면 됩니다.
- n은 1 이상, 2000 이하인 정수입니다.
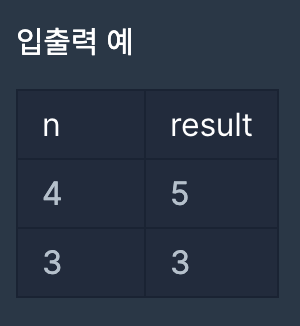
입출력 예 설명
입출력 예 #1
위에서 설명한 내용과 같습니다.
입출력 예 #2
(2칸, 1칸)
(1칸, 2칸)
(1칸, 1칸, 1칸)
총 3가지 방법으로 멀리 뛸 수 있습니다.
풀이
왜 3점 씩이나 주는지 모르겠는 문제다.
dp 문제인데 내가 쉽게 풀 수 있는 dp는 쉬운 문제이다.
왜 쉽냐면 n = 1~5일 때를 직접 구해보면 1 , 2, 3, 5, 8이다.
맞다.
피보나치다.
끝..이 아니라 그래도 규칙을 좀 얘기해 보자면
n=1
1
n=2
1 1 (n=1 +1)
2 (n=0 +2)
n=3
1 1 1 (n=2 +1)
2 1 (n=2 +1)
1 2 (n=1 +2)
n=4
1 1 1 1 (n=3 +1)
1 2 1 (n=3 +1)
2 1 1 (n=3 +1)
1 1 2 (n=2 +2)
2 2 (n=2 +2)
즉 n=4는 n=2인 경우에 2를 더한 값들 + n=3인 경우에 1을 더한 값들로
dp[n] = dp[n-1] + dp[n-2] 이란 점화식이 나온다.
코드
//피보나치
class Solution {
fun solution(n: Int): Long {
var dp = LongArray(n+1)
dp[0]=1
dp[1]=1
if(n<2) return dp[n]
for(i in 2 ..n){
dp[i] = (dp[i-1]+dp[i-2])%123_456_7
}
return dp[n]
}
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 6087 레이저 통신 Kotlin (다익스트라) (0) | 2022.04.26 |
|---|---|
| 백준 12886 돌 그룹 Kotlin (bfs) (0) | 2022.04.24 |
| 백준 16198 에너지 모으기 Kotlin (순열) (0) | 2022.04.22 |
| 백준 15658 연산자 끼워넣기 (2) Kotlin (순열) (0) | 2022.04.21 |
| 백준 16197 두 동전 Kotlin (bfs) (0) | 2022.04.20 |




댓글