백준 4690 완전 세제곱 Kotlin (완전탐색)

문제 출처 : https://www.acmicpc.net/problem/4690

4690번: 완전 세제곱

문제

페르마의 마지막 정리는, a, b, c가 0이 아닌 정수이고, n이 2보다 큰 자연수 일 때, an = bn + cn을 만족하는 자연수 a, b, c가 존재하지 않는다는 정리이다. 이 정리는 아직 증명되지 않았다.

하지만, 완전 세제곱 방정식 a3 = b3 + c3 + d3을 만족하는 1보다 큰 자연수를 찾는 것은 어렵지 않다. (123 = 63 + 83 + 103)

이러한 완전 세제곱 방정식과 a ≤ 100을 만족하는 {a, b, c, d}쌍을 모두 찾는 프로그램을 작성하시오.

입력

이 문제는 입력이 없다.

출력

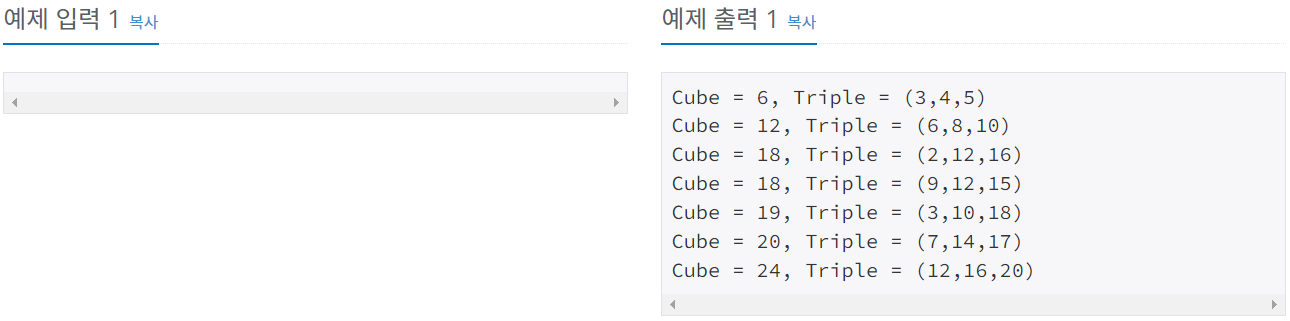
a값이 증가하는 순서대로 아래 출력 형식과 같이 출력한다. b, c, d도 증가하는 순서로 이루어져야 한다. a값에 해당하는 b, c, d쌍이 여러 개 존재할 수 있다. 이때는 b 값이 작은 것부터 먼저 출력한다.

아래 출력 예제는 일부분만 나와있다.

노트

페르마의 마지막 정리는 1995년에 앤드루 와일스에 의해 증명되었다.

알고리즘 분류

• 수학
• 구현
• 브루트포스 알고리즘
• 런타임 전의 전처리

풀이

간단한 완전 탐색 문제이다.

주어진 조건대로 구현만 하면 되는데,

a는 2부터 100까지,

b는 1부터 100까지,

c는 b+1부터 100까지

d는 c+1부터 100까지

모든 경우를 검사하면 된다.

 

코드

val br = System.`in`.bufferedReader()

fun main() = with(System.out.bufferedWriter()){

    for(a in 2 .. 100) {
        val left = a * a * a
         for (b in 2..100) {
             for (c in b + 1..100) {
                for (d in c + 1..100) {
                    val right = b * b * b + c * c * c + d * d * d
                    if (left < right) break
                    if (left == right) {
                        write("Cube = $a, Triple = ($b,$c,$d)\n")
                        break
                    }
                }
            }
        }
    }
    close()
}