문제 출처 : https://www.acmicpc.net/problem/16288
16288번: Passport Control
입력은 표준입력을 사용한다. 첫 번째 줄에는 두 개의 정수 N 과 k 가 주어진다. N은 입국 승객의 수이며 k는 여권 심사 창구의 수이다. 단, 2 ≤ k ≤ N ≤ 100 이다. 그리고 두 번째 줄에는 승객이 입
www.acmicpc.net

문제
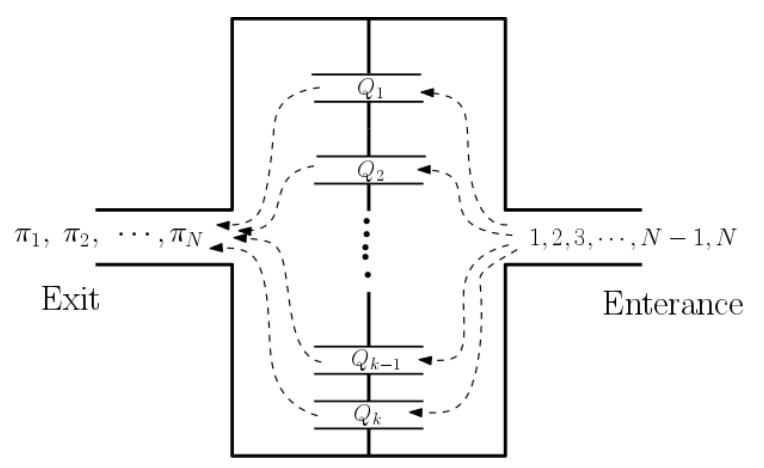
그림 G.1: N명의 입국 승객은 k개의 여권 심사 창구 {Qk} 중 하나를 반드시 거쳐야 한다.
N명의 입국 승객이 여권 심사를 위하여 그림 G.1 과 같이 입국 대기 줄에서 [1, 2, … , N − 1, N] 순서로 기다리고 있다. 입국 승객은 준비된 k개의 여권 심사 창구 중 하나를 통과한 뒤 공항을 빠져나갈 수 있다. 입국할 때의 줄 선 승객의 순서를 [1, 2, … , N − 1, N]이라고 할 때 k개의 여권 심사 창구를 통과하여 입국장을 빠져나가는 순서 [π1, π2, … πN−1, πN]는 처음과 달라질 수 있다. k개 여권 심사 창구가 준비되어 있을 때, 이 입국장을 빠져나가는 순서가 가능한 순서인가를 계산해야 한다.
예를 들어 설명해보자. 만일 N = 3, k = 2라고 할 때 입국장을 빠져나가는 순서 중 [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]는 가능하지만 [3, 2, 1]은 불가능하다. 여러분은 입국장을 빠져나가는 순서 [π1, … , πN]가 입력으로 주어질 때, 이 순서가 가능하면 YES 를, 불가능하면 NO 를 출력해야 한다. 단, 특정 큐에 줄을 선 상황에서는 승객들의 순서를 임의로 바꿀 수는 없다. 그리고 각 여권 심사 창구에 준비된 큐는 N명 승객이 모두 들어올 정도로 충분히 크다고 가정한다.
입력
입력은 표준입력을 사용한다. 첫 번째 줄에는 두 개의 정수 N 과 k 가 주어진다. N은 입국 승객의 수이며 k는 여권 심사 창구의 수이다. 단, 2 ≤ k ≤ N ≤ 100 이다. 그리고 두 번째 줄에는 승객이 입국장을 빠져 나가는 순서 [π1, … , πN]가 주어진다.
출력
출력은 표준출력을 사용한다. 입력으로 주어진 순서 [π1, … , πN]대로 입국장을 빠져나가는 것이 가능하면 YES 를 출력하고, 아니면 NO 를 출력해야 한다.
알고리즘 분류
풀이
왜 알고리즘 분류에 다이나믹 프로그래밍이 있는지는 잘 모르겠다.
가장 긴 증가하는 부분 수열을 구하라는 의미인가?
그럴 필요는 없다.
처음엔 갈피를 못 잡아서 구글링으로 풀이를 참고했다.
본인의 풀이는 다음과 같다.
예제 2를 보면 창구는 총 3개이고, 검사해야 하는 입력은
4 1 3 2 5 6 8 9 7 10이다.
창구는 큐와 같은 FIFO(선입 선출)구조이다.
1~n번까지의 사람이 순서대로 들어가기 때문에, 모든 창구는 증가수열임을 알 수 있다!
즉, 주어진 입력에서 k개의 창구가 모두 증가수열을 이룰 수 있다면 YES, 없다면 NO다.
예제 2의 증가수열의 수를 2중 for문으로 구하면
4 1 3 2 5 6 8 9 7 10
3개의 증가수열이 나온다. 즉 3개의 창구로 위의 순서가 가능하단 얘기다.
증가수열의 개수를 구하지 않고도 정답을 찾을 수 있다.
우선 창구를 1차원 Int 배열로 만들고, 이 배열엔 가장 최근에 각 창구에 들어간 값을 저장한다.
arr[i] = j // i창구에 가장 최근에 들어간 값 j
입력의 순서대로 k개의 창구에 값을 넣는데, 창구에 있는 값이 들어갈 값보다 작은 경우만 들어갈 수 있다.
만약 현재 값을 k개의 창구에 모두 넣을 수 없을 때 답은 NO이다.
코드
val br = System.`in`.bufferedReader()
fun main() = with(System.out.bufferedWriter()){
val (n,k) = br.readLine().split(' ').map{it.toInt()}
val arr = br.readLine().split(' ').map{it.toInt()}.toIntArray()
var cnt=0
for(i in 0 until n){
if(arr[i]==0) continue
var pre = arr[i]
arr[i]=0
for(j in i+1 until n){
if(pre<arr[j]){
pre=arr[j]
arr[j]=0
}
}
cnt++
}
if(cnt<=k) write("YES") else write("NO")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 16956 늑대와 양 Kotlin (구현) (0) | 2021.12.29 |
|---|---|
| 백준 17425 약수의 합 Kotlin (에라토스테네스의 체, 누적 합) (0) | 2021.12.29 |
| 백준 16982 뱀과 사다리 게임 Kotlin (bfs) (0) | 2021.12.29 |
| 백준 9019 DSLR Kotlin (bfs) (0) | 2021.12.28 |
| 백준 14658 하늘에서 별똥별이 빗발친다 Kotlin (완전탐색) (0) | 2021.12.28 |




댓글