
환경 : Kotlin Version = 1.5.20, Java version = 14.0.2 JVM, Android Studio
Kotlin/Java의 sort 동작 방식 알아보기
0. 결론
글이 길어져서 결론부터 말하자면, 코틀린과 자바에서
Arrays.sort는 Dual-Pivot QuickSort
Collections.sort는 TimSort
를 사용한다.
실제로는 Counting Sort, Merge Sort 등등의 정렬을 휴리스틱한 방법으로, 적재적소에 사용한다.
Dual-Pivot QuickSort = Quick Sort
Best : O(NlogN)
average : O(NlogN)
worst : O(N^2)
TimSort = Insertion Sort + Merge Sort, 시간 복잡도는
Best : O(N)
average : O(NlogN)
worst : O(NlogN)
아래에 왜 Array는 Dual-Pivot QuickSort이고 Collection은 Tim Sort를 사용하는지 추가로 작성해 두었다.
1. sort 함수?
대부분의 언어는 리스트를 정렬해주는 sort 함수를 제공한다.
이전, 알고리즘 문제를 풀기 위해 c++을 공부한 적이 있는데,
그때 c++의 STL 인 Algorithm 헤더의 sort()의 동작 방식과 시간 복잡도가 궁금해서 찾아본 적이 있다.
찾아본 결과, c++의 sort()는 퀵 정렬 기반이며, 퀵 정렬은 최악의 경우 O(N^2)의 시간 복잡도를 가진다는 단점이 있다.
하지만, c++ sort()는 이를 보완하는 장치가 있다고 한다.
이 정도로만 알고 사용해왔었는데, Java와 Kotlin으로 주로 개발하고 요즘은 또 Kotlin으로 알고리즘 문제를 풀기 때문에
이번엔 어느 정도 자세히! Java와 Kotlin의 sort 방식을 알아보기로 했다.
아래에서 나올 3가지 well-known 정렬에 관한 글이다.
2021.07.18 - [알고리즘] - [알고리즘] 삽입 정렬 (Insertion Sort)
2021.07.19 - [알고리즘] - [알고리즘] 퀵 정렬(Quick Sort)
2021.07.21 - [알고리즘] - [알고리즘] 병합/합병 정렬(Merge Sort)
2. 코틀린과 자바의 정렬 방식


코틀린에서 sort함수를 따라가 보면 내부적으로 java.util.Arrays.sort를 호출하는 것을 알 수 있다.
위에는 그냥 primitive 데이터를 사용하는 Arrays.sort였지만,
Collections.sort는 어떨까?



마찬가지로 결국 ArraysJvm에서 java.util.Arrays.sort를 호출하는 것을 알 수 있다.
역시나 코틀린은 자바의 정렬 방식을 그대로 사용한다.
따라서 Arrays.java 파일을 뜯어봐서 오늘의 궁금점을 해결하기로 했다.


Arrays.java 클래스에 대한 설명이다.
검색, 정렬 등 배열을 다루기 위한 다양한 메소드가 포함되어있고, 오라클에서 docs를 볼 수 있다고 한다.
본인은 그냥 코드로 보겠다.

java는 크게 Dual-Pivot QuickSort 와 TimSort 방식을 사용한다.
sort의 매개 변수 타입이 다른 걸 볼 수 있는데,
Dual-Pivot QuickSort는 primitive(기본형) 데이터들을 정렬하는 데에 사용하고,
TimSort는 references(객체,참조) 데이터들을 정렬하는 데에 사용한다.
즉 Arrays.sort는 Dual-Pivot QuickSort
Collections.sort는 TimSort를 사용한다.
2021.08.10 - [언어/Kotlin&Java] - [코틀린/Kotlin] 기초 #04_기본형 vs 참조형
과거에는 Merge Sort, Quick Sort, Insertion Sort 세 가지를 적절하게 나누어 사용했지만,
현재는 이들을 혼합하여
Merge Sort + Insertion Sort = TimSort
그리고 Dual-Pivot Quick Sort
를 사용한다고 한다.
Merge Sort와 Quick Sort는 평균 O(NlogN)의 시간 복잡도를 가져 빠른 정렬에 속하지만,
Insertion Sort는 평균 O(N^2)의 시간 복잡도인데 왜 같이 사용하는 걸까?
Insertion Sort는 이전 포스팅 글과, 위키 백과를 참고하자.
아직 잘 모르겠다.
Insertion Sort는 이미 정렬된 배열을 가져왔을 때는 O(N)의 시간 복잡도를 갖는 것에 관련이 있을 것 같다.
이 부분에 대해서는 Dual-Pivot QuickSort 와 TimSort에 대해 파헤쳐보면서 추후에 더 다루어보도록 하자.
3. Dual-Pivot QuickSort
Best : O(NlogN)
average : O(NlogN)
worst : O(N^2)
시간 복잡도는 QuickSort와 같다.
여전히 최악의 경우 O(N^2)이지만, 기존 퀵 정렬보단 효율적이라고 한다.
단일 피벗을 사용하는 기존 퀵 정렬과 달리, 이름처럼 두 개의 피벗을 사용한다.
DualPivotQuickSort.java
/*
* Tuning parameters.
*/
/**
* The maximum number of runs in merge sort.
*/
private static final int MAX_RUN_COUNT = 67;
/**
* The maximum length of run in merge sort.
*/
private static final int MAX_RUN_LENGTH = 33;
/**
* If the length of an array to be sorted is less than this
* constant, Quicksort is used in preference to merge sort.
*/
private static final int QUICKSORT_THRESHOLD = 286;
/**
* If the length of an array to be sorted is less than this
* constant, insertion sort is used in preference to Quicksort.
*/
private static final int INSERTION_SORT_THRESHOLD = 47;
/**
* If the length of a byte array to be sorted is greater than this
* constant, counting sort is used in preference to insertion sort.
*/
private static final int COUNTING_SORT_THRESHOLD_FOR_BYTE = 29;
/**
* If the length of a short or char array to be sorted is greater
* than this constant, counting sort is used in preference to Quicksort.
*/
private static final int COUNTING_SORT_THRESHOLD_FOR_SHORT_OR_CHAR = 3200;Dual-Pivot QuickSort의 코드이다.
Tuning parameter들에 대한 정의인데,
Primitive type 정렬은 Dual-Pivot QuickSort를 사용한다고 했는데,
사실 내부에선 이렇게 제한을 두고 heuristic한 방법으로 상황에 맞게 적절한 정렬 기법을 사용한다.
예를 들어서 byte 외에 모든 Primitive type은 길이가 47을 넘지 않으면 Insertion Sort를 사용하고,
byte, short는 길이가 29를 넘고, char는 길이가 3200을 넘는 경우 Counting Sort(계수 정렬)을 사용한고,
어느 정도 이미 정렬된 리스트는 Quick Sort가 아닌 Merge Sort를 사용한다.
즉, Dual-Pivot QuickSort는 내부적으로 최소 4개 이상의 정렬 기법들을 적절한 상황에 사용한다.
Dual-Pivot QuickSort 코드
/*
* Sorting methods for seven primitive types.
*/
/**
* Sorts the specified range of the array using the given
* workspace array slice if possible for merging
*
* @param a the array to be sorted
* @param left the index of the first element, inclusive, to be sorted
* @param right the index of the last element, inclusive, to be sorted
* @param work a workspace array (slice)
* @param workBase origin of usable space in work array
* @param workLen usable size of work array
*/
static void sort(int[] a, int left, int right,
int[] work, int workBase, int workLen) {
// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {
sort(a, left, right, true);
return;
}
/*
* Index run[i] is the start of i-th run
* (ascending or descending sequence).
*/
int[] run = new int[MAX_RUN_COUNT + 1];
int count = 0; run[0] = left;
// Check if the array is nearly sorted
for (int k = left; k < right; run[count] = k) {
if (a[k] < a[k + 1]) { // ascending
while (++k <= right && a[k - 1] <= a[k]);
} else if (a[k] > a[k + 1]) { // descending
while (++k <= right && a[k - 1] >= a[k]);
for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
}
} else { // equal
for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {
if (--m == 0) {
sort(a, left, right, true);
return;
}
}
}
/*
* The array is not highly structured,
* use Quicksort instead of merge sort.
*/
if (++count == MAX_RUN_COUNT) {
sort(a, left, right, true);
return;
}
}
// Check special cases
// Implementation note: variable "right" is increased by 1.
if (run[count] == right++) { // The last run contains one element
run[++count] = right;
} else if (count == 1) { // The array is already sorted
return;
}
// Determine alternation base for merge
byte odd = 0;
for (int n = 1; (n <<= 1) < count; odd ^= 1);
// Use or create temporary array b for merging
int[] b; // temp array; alternates with a
int ao, bo; // array offsets from 'left'
int blen = right - left; // space needed for b
if (work == null || workLen < blen || workBase + blen > work.length) {
work = new int[blen];
workBase = 0;
}
if (odd == 0) {
System.arraycopy(a, left, work, workBase, blen);
b = a;
bo = 0;
a = work;
ao = workBase - left;
} else {
b = work;
ao = 0;
bo = workBase - left;
}
// Merging
for (int last; count > 1; count = last) {
for (int k = (last = 0) + 2; k <= count; k += 2) {
int hi = run[k], mi = run[k - 1];
for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
b[i + bo] = a[p++ + ao];
} else {
b[i + bo] = a[q++ + ao];
}
}
run[++last] = hi;
}
if ((count & 1) != 0) {
for (int i = right, lo = run[count - 1]; --i >= lo;
b[i + bo] = a[i + ao]
);
run[++last] = right;
}
int[] t = a; a = b; b = t;
int o = ao; ao = bo; bo = o;
}
}Dual-Pivot Quicksort는 boolean을 제외한 7가지 primitive type를 정렬한다.
위 코드는 그중 int 배열을 정렬하기 위한 메소드 중 한 부분인데, 코드가 너무 길어서 접어놨다.
오늘은 어떤 알고리즘으로 동작하는지에 대해 알아보기 위함이기 때문에
다음에 정형적인 Dual-Pivot QuickSort의 동작 방식을 분석 및 구현해 보겠다.
4. TimSort
Best : O(N)
average : O(NlogN)
worst : O(NlogN)

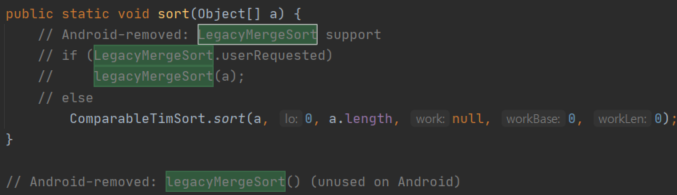
이번엔 TimSort 코드이다.
아니 코드라기보단 설명이다.
핵심은 stable sort이며 기존 Merge Sort보다 훨씬 적응적이고 적은 반복의 병합 정렬이라 한다.
또한, 기존 Merge Sort보다 작은 공간이 필요하다고 한다.
public static void sort(Object[] a) {
// Android-removed: LegacyMergeSort support
// if (LegacyMergeSort.userRequested)
// legacyMergeSort(a);
// else
ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
}
// Android-removed: legacyMergeSort() (unused on Android)위에서 Merge Sort, Quick Sort, Insertion Sort 세 가지를 적절하게 나누어 사용했지만,
현재는 이들을 혼합하여 사용한다고 했는데, 이에 대한 근거이다.
TimSort는 팀 피터스(Tim Peters)에 의해 파이썬 언어에 사용하기 위한 정렬 방법으로 발명되었고,
조쉬 블로흐(Josh Bloch)가 자바로 포스팅하였다.
jdk7 이상부터는 Arrays.sort 실행 시 TimSort로 정렬하고,
jdk6 이하부터는 LegacyMergeSort로 정렬된다.
jdk7 이상에서도 기존 병합 정렬로 동작하고 싶으면 어떠한 설정이 필요한데, 굳이??
6. TimSort vs Dual-Pivot QuickSort
위에서 heuristic하게 적절한 정렬 방식을 사용한다고 했다.
즉, 상황에 따라 효율적인 정렬 방식을 제공한다.
그렇다면 왜 Arrays와 Collections의 정렬 방식이 다를까?
결론부터 말하면 Unstable vs Stable이다. (수정된 결론)
Merge Sort보다 Quick Sort가 일반적으로 빠르다는 걸 알고 있을 것이다.
시간 복잡도만 본다면 Merget Sort가 더 성능이 좋아야 하지만, 시간 복잡도는 수학적인 이론이다.
실제 알고리즘의 구현은 컴퓨터라는 하드웨어에서 돌아가고, 수학적인 개념에서는 메모리 생성/삭제/복사 등의 연산 수행 시간을 고려하지 않기 때문에 현실적인 제약들에 의해서 Quick Sort가 일반적으로 더 효율적이라고 할 수 있는 것이다.
시간 복잡도가 O(NLogN)일때 실제 동작 시간은 C * NlogN + α이다.
+ α는 더하는 값이니 상대적으로 무시할 수 있지만,
C는 곱하는 값이니 실제 동작 시간에 큰 영향을 끼친다.
이 C라는 값에 큰 영향을 끼치는 요소로는 '알고리즘이 참조 지역성 원리를 얼마나 잘 만족하는가'가 있다.
참조 지역성 원리란 CPU가 미래에 원하는 데이터를 예측하여 속도가 빠른 장치인 캐시 메모리에 담아 놓는데 이때의 예측률을 높이기 위해 사용하는 원리이다.
데이터 예측이란, 최근에 참조한 메모리나 그 메모리와 인접한 메모리를 다시 참조할 확률이 높다는 이론으로 캐시 메모리에 담아놓는 것이다. 따라서, 메모리를 연속으로 읽는 작업은 캐시 메모리에서 읽어오기에 빠르지만, 무작위로 읽는 작업은 메인 메모리에서 읽어오기 때문에 속도의 차이가 발생한다.
다시 Arrays와 Collections으로 돌아오면, Arrays는 각 값들이 연속적인 주소를 가지고 있으니 참조 지역성이 좋다고 할 수 있고, Collections은 메모리가 연속적이지 않은 LinkedList 등이 존재하기 때문에, 참조 인접성이 좋지 않다고 할 수 있다. 따라서 Arrays는 C가 낮은 편이고, Collections는 C가 높은 편인데, 이러한 상황에 따라 가장 효율적인 정렬 방식을 택하게 된 것이다.
왜 C가 높을 땐 TimSort가 효율적이고, C가 낮을 땐 Dual-Pivot QuickSort가 효율적인지는 두 알고리즘의 동작 방식을 분석하면 알 수 있을 것 같다.
2022.10.17 수정
최근 dual pivot quick sort와 tim sort를 다시 공부했는데, 위 내용은 틀린 것 같다. 혹시나 이 글을 자세히 읽으신 분이 있다면 죄송..
우선 dual pivot quick sort의 배경은 quick sort의 최적화다.
quick sort는 O(nlogn) 비교 정렬 중 가장 빠르다고 알려졌지만 최악의 경우 (이미 정렬된 경우) O(n^2)의 시간 복잡도를 갖는다.
따라서 quick sort는 pivot을 어떻게 설정하느냐에 따라 최적화할 수 있는데, 왼쪽, 오른쪽, 가운데만 비교한다면 리스트의 가운데를 pivot으로 설정하는 것이 가장 빠르다.
실제 수행 시간을 찍어봐도 되고, 아래 백준 문제는 pivot을 왼쪽으로 설정했을 때는 시간 초과, pivot을 가운데로 설정했을 때는 통과이다.
https://www.acmicpc.net/problem/10989
하지만 이것만으론 부족하다. 더 최적화 할 방법이 없을까?
해서 나온 것이 dual pivot quick sort이다.
dual pivot quick sort는 left pivot, right pivot 두 개의 pivot을 설정한다.
lp = x (left pivot에 위치한 값)
rp = y (right pivot에 위치한 값)
| lp보다 작은 값들 | lp | lp보다 크고 rp보다 작은 값들 | rp | rp보다 큰 값들 |
위와 같은 방식으로 최적화한 것이 dual pivot quick sort이다.
Tim sort는 무엇인가?
Tim sort의 배경은 위에서 말한 '참조 지역성 원리를 얼마나 만족하는가'(이하 C)와 관련이 있다.
더 빠른 정렬을 위해선 기존 C * O(nlogn) + α 에서 nlogn의 실제 동작을 줄이는 것도 중요하고, C를 줄이는 것도 중요하다.
즉, C와 nlogn의 시간 복잡도를 줄이기 위해 merge sort에 insertion sort를 합쳐서 최적화한 것이 Tim sort이다.
근데 왜 하필 insertion sort일까?
insertion sort의 정렬 방식을 생각해 보면 주변 인덱스를 참조하며 비교한다.
이와 반대되는 예시는 heap sort이다. (인덱스의 2배 혹은 1/2배 인덱스를 비교한다)
따라서 insertion sort는 C값이 작다. (참조 지역성 원리를 잘 만족한다)
하지만 여전히 bubble sort나 selection sort를 생각해보아도 이들도 근접한 인덱스를 비교하기 때문에 참조 지역성 원리를 어느 정도 잘 만족하므로 큰 메리트가 없다고 느껴지지만, insertion sort는 최적의 경우 O(N)의 시간 복잡도를 갖는다. 실제로 정렬 동작을 O(N^2) 비교 정렬 중에선 가장 적은 동작을 하기 때문에 insertion sort가 채택된 것이다.
Tim sort는 2^2x개씩 각각 잘라 Insertion sort로 정렬하면 일반적인 merge sort보다 덩어리별 x개의 병합 동작이 생략되어 최종적으로 동작 시간은 merge sort의 C값을 C(m)이라 했을 때 C(m) * O(nlogn-x) + α 가 되는 것이다.
이에 대한 자세한 내용은 아래 네이버 D2 블로그에서 확인할 수 있다.
https://d2.naver.com/helloworld/0315536
자, 이제 dual pivot quick sort 와 tim sort에 대해선 알겠다.
그래서 왜 Array는 dual pivot quick sort, Collection은 tim sort인가?
그것은 stable vs unstable이라고 할 수 있다.
quick sort는 입력 순서를 보장하지 않는 unstable 정렬이고
merge sort 와 insertion sort는 stable 정렬이다.
따라서 dual pivot quick sort는 unstable
tim sort는 stable이다.
우리가 코틀린에서 사용하는 기본 Array들
IntArray, LongArray 등이 있다.
val arr = intArrayOf(5,1,3,1,2)
val sortedArr = intArrayOf(1,1,2,3,5)위의 코드로 봤을 때 우리는 두 개의 '1'이란 원소에 대해 입력 순서가 중요한가?
기본 자료형은 값만 중요하기 때문에 입력 순서가 중요하지 않다.
따라서 정렬할 때 stable을 고려하지 않아도 된다.
(예외로 Array<T>는 Collections.sort로 동작한다. 이것도 약간의 힌트다.)
Collection 같은 경우에는 기본 자료형 뿐만 아니라 클래스도 원소로 사용할 수 있다.
data class Person(
val age: Int,
val height: Int
)
fun main(){
val list = mutableListOf<Person>(
Person(age = 3, height = 10),
Person(age = 1, height = 20),
Person(age = 1, height = 30)
)
val stableSortedArr1 = mutableListOf<Person>(
Person(age = 1, height = 20),
Person(age = 1, height = 30),
Person(age = 3, height = 10)
)
val unstableSortedArr2 = mutableListOf<Person>(
Person(age = 1, height = 30),
Person(age = 1, height = 20),
Person(age = 3, height = 10)
)
}위 코드를 보면 age를 기준으로 오름차순 정렬했을 때 stable이냐 unstable이냐에 따라 정렬 결과가 달라질 수 있음을 알 수 있다.
따라서 Collection에서는 입력 순서를 고려해야 하기 때문에 stable한 tim sort를 사용하게 되는 것이다.
역시 기본 자료형은 여러모로 퍼포먼스 면에서 뛰어날 수 밖에 없는 것 같다.
7. 마치며
Java와 Kotlin에서 sort가 어떤 방식을 채택했는지 알 수 있었다.
추후에, Dual-Pivot QuickSort와, TimSort 알고리즘을 분석하여 포스팅할 예정이다.
다만, 언제가 될진 모르겠다.
생각보다 포스팅하는 데에 시간이 많이 소요된다..
8. References
http://egloos.zum.com/js7309/v/11164744
https://d2.naver.com/helloworld/0315536
https://www.geeksforgeeks.org/timsort/?ref=gcse
https://www.geeksforgeeks.org/dual-pivot-quicksort/?ref=gcse
https://stackoverflow.com/questions/4018332/is-java-7-using-tim-sort-for-the-method-arrays-sort
TODO
Dual-Pivot QuickSort 알고리즘 분석
TimSort 알고리즘 분석
'언어 > Kotlin&Java' 카테고리의 다른 글
| [코틀린/Kotlin] 기초 #07_코틀린의 연산자 (0) | 2021.08.17 |
|---|---|
| [코틀린/Kotlin] 기초 #06_자료형 변환과 스마트 캐스트 (0) | 2021.08.15 |
| [코틀린/Kotlin] 기초 #05_ 안전한 null 처리 (0) | 2021.08.14 |
| [Kotlin/Java] Android Studio에서 테스트 환경 구축하기_2 (0) | 2021.08.13 |
| [Kotlin/Java] Android Studio에서 테스트 환경 구축하기_1(수정) (0) | 2021.08.12 |




댓글