문제 출처 : https://www.acmicpc.net/problem/14500
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net

문제
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
- 정사각형은 서로 겹치면 안 된다.
- 도형은 모두 연결되어 있어야 한다.
- 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
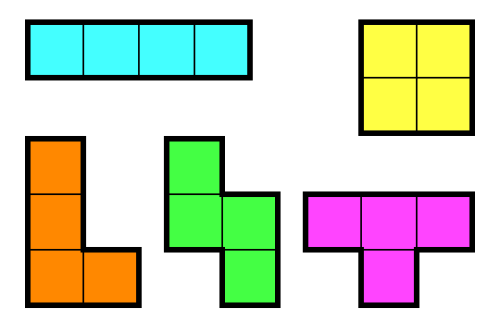
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.

알고리즘 분류
풀이
완전 탐색 기반 dfs 문제이다.
우선 문제를 보면 주어진 테트로미노들을 회전하고 뒤집고 할 생각에 좀 스트레스 받지만,
이젠 이런 문제의 대처법을 안다.
간혹가다, 모든 경우를 구현해야 하는 문제도 있지만, 보통은 이렇게 구현해야 할 것이 많으면, 이들의 공통된 규칙이 발견된다.
테트로미노들을 보면 모두 4칸인 걸 알 수 있고, ㅗ 모양을 제외하면, 한 점에서 뎁스4인 깊이 우선 탐색으로 구할 수 있는 것을 알 수 있다.
처음엔 대칭이란 단어를 못 보고, 회전만 시킬 수 있는 줄 알아서 한 점에서 탐색을 시작하되 가지치기를 통해 주어진 테트로미노들의 회전된 모양들만 탐색하는 방법을 찾으려 했지만, 답이 없었고, 문제를 다시 보니 대칭이란 말이 있었다.
회전과 대칭이 가능한 이 테트로미노 모양들은 한 점에서 dfs를 통해 뎁스 4까지 탐색하는 모든 경로들과 같다.
즉, 모든 칸에 대해 ㅗ를 제외한 모양들을 dfs로 4뎁스까지 탐색하고, ㅗ모양은 따로 확인해 주는 것으로 구현을 최소화할 수 있다.
dfs의 구현은, 매번 한 칸에 대해 dfs를 시작할 때마다 visited배열을 초기화하는 것이 아닌, dfs의 특징을 살려 다음 뎁스로 넘어가기 전 visited[nextR][nextC]를 체크하고, 다시 돌아올 때 visited[nextR][nextC]를 해제하는 방법을 사용할 수 있다. 뎁스가 깊어질 때마다 방문한 칸은 체크해야 하지만, 하나의 테트로미노(한 번의 뎁스4까지 탐색)이 끝나면 다시 방문했던 칸을 방문해야 하는 일이 일어나기 때문에 다시 체크를 해제해야 하는 것이다.
이렇게 dfs는 방문했던 칸을 쉽게 되돌아갈 수 있기 때문에, bfs로는 구현이 힘들고 dfs로 하는 것이 알맞다.
즉, 어떤 노드의 유망성을 점검한 후, 유망하지 않으면 다시 부모 노드로 돌아가는 dfs에 속하는 백트래킹 알고리즘이라 할 수 있다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//4<=n,m<=400
int n, m;
int graph[500][500];
int dir[4][2] = { {0,1} ,{0,-1},{1,0},{-1,0} };
bool visited[500][500];
int answer;
bool isInside(int r, int c) {
if (r < 0 || r >= n || c < 0 || c >= m) return false;
return true;
}
void reset() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
visited[i][j] = false;
}
}
}
void dfs(int r, int c, int depth, int sum) {
if (depth == 3) {
answer = max(answer, sum);
return;
}
for (int i = 0; i < 4; i++) {
int nR = r + dir[i][0];
int nC = c + dir[i][1];
if (!isInside(nR, nC))continue;
if (visited[nR][nC])continue;
visited[nR][nC] = true;
dfs(nR, nC, depth + 1, sum + graph[nR][nC]);
visited[nR][nC] = false;
}
}
void shape1(int r, int c)
{
int sum = 0;
sum = graph[r][c] + graph[r][c + 1] + graph[r][c + 2] + graph[r - 1][c + 1];
answer = max(answer, sum);
}
void shape2(int r, int c)
{
int sum = 0;
sum = graph[r][c] + graph[r][c + 1] + graph[r][c + 2] + graph[r + 1][c + 1];
answer = max(answer, sum);
}
void shape3(int r, int c)
{
int sum = 0;
sum = graph[r][c] + graph[r + 1][c] + graph[r + 2][c] + graph[r + 1][c + 1];
answer = max(answer, sum);
}
void shape4(int r, int c)
{
int sum = 0;
sum = graph[r][c] + graph[r - 1][c + 1] + graph[r][c + 1] + graph[r + 1][c + 1];
answer = max(answer, sum);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
answer = 0;
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> graph[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
visited[i][j] = true;
dfs(i, j, 0, graph[i][j]);
visited[i][j] = false;
if (i - 1 >= 0 && j + 2 < m) shape1(i, j);
if (j + 2 < m && i + 1 < n) shape2(i, j);
if (i + 2 < n && j + 1 < m) shape3(i, j);
if (i + 1 < n && i - 1 >= 0 && j + 1 < m) shape4(i, j);
}
}
cout << answer;
return 0;
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2668 숫자고르기 c++ (dfs) (0) | 2021.10.30 |
|---|---|
| 백준 2512 예산 c++ (이분 탐색) (0) | 2021.10.28 |
| 백준 1663 XYZ 문자열 c++ (dp) (0) | 2021.10.26 |
| 백준 21315 카드 섞기 c++ (완전탐색) (0) | 2021.10.25 |
| 백준 15661 링크와 스타트 c++ (완전탐색) (5) | 2021.10.24 |




댓글