문제 출처 : https://www.acmicpc.net/problem/1725
1725번: 히스토그램
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은
www.acmicpc.net

문제
히스토그램에 대해서 알고 있는가? 히스토그램은 아래와 같은 막대그래프를 말한다.
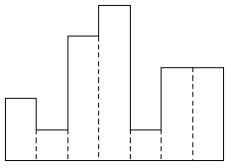
각 칸의 간격은 일정하고, 높이는 어떤 정수로 주어진다. 위 그림의 경우 높이가 각각 2 1 4 5 1 3 3이다.
이러한 히스토그램의 내부에 가장 넓이가 큰 직사각형을 그리려고 한다. 아래 그림의 빗금 친 부분이 그 예이다. 이 직사각형의 밑변은 항상 히스토그램의 아랫변에 평행하게 그려져야 한다.
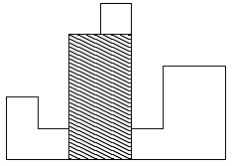
주어진 히스토그램에 대해, 가장 큰 직사각형의 넓이를 구하는 프로그램을 작성하시오.
입력
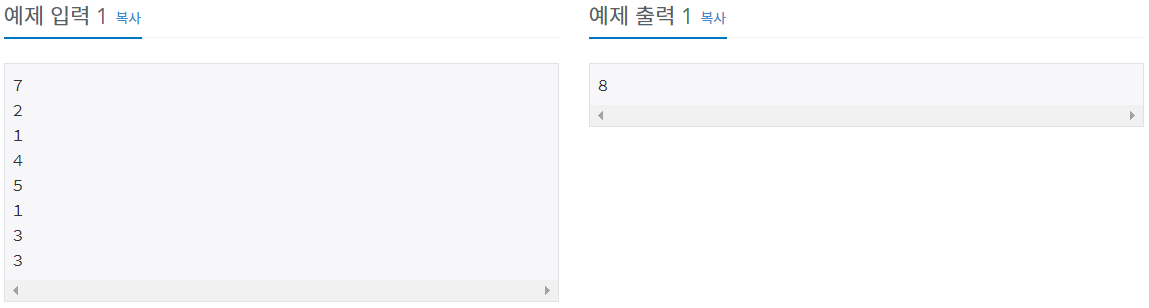
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄에 가장 큰 직사각형의 넓이를 출력한다. 이 값은 20억을 넘지 않는다.
알고리즘 분류
풀이
해당 문제 풀이의 핵심은 다음과 같다.
1. 주어진 막대들의 인덱스를 스택에 차례대로 쌓는다.
2. i번째 막대의 인덱스를 스택에 쌓을 때, 현재 스택의 가장 윗부분에 있는 막대보다 i번째 막대의 높이가 더 높거나
같다면 계속 쌓는다.
3. i번째 막대의 인덱스를 스택에 쌓을 때, 현재 스택의 가장 윗부분에 있는 막대보다 i번째 막대의 높이가 더 짧다면
스택의 가장 윗부분에 있는 막대가 i번째 막대의 높이보다 짧거나 같아질 때까지 stack을 하나씩 pop하며 사각형의
넓이를 구한다.
** 주어진 막대그래프의 맨 앞, 맨 뒤에 높이가 0인 막대를 추가하면 모든 경우의 수를 구할 수 있다.
넓이의 최댓값을 구하는 코드는 다음과 같다.
answer = max(answer,high[highIdx]*(i-stk.peek()-1))
//highIdx = 스택의 가장 위에 있던 막대의 인덱스
//high = 막대의 높이를 저장하는 배열
//stk = 스택
//i = 현재 검사하는 막대의 인덱스
우선 높이는 더 짧은 막대를 만났을 때(i), 스택의 가장 위에 있는 막대의 인덱스를 pop해서 highIdx에 저장하고,
high[highIdx]로 검사할 직사각형의 가장 높은 높이를 구할 수 있다.
넓이는 현재 검사하는 인덱스 i에서 highIdx를 구하고 남은 스택의 가장 위에 있는 막대의 인덱스만큼을(stk.peek()) 빼고
1을 더 빼주면 된다.
위의 과정으로 주어진 예시의 답을 찾아보자.
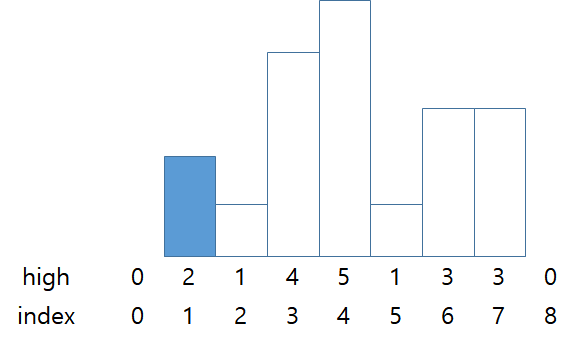
stack = {0,1}
초기에 스택에 0을 넣어놓고, 2는 0보다 높기 때문에 스택에 높이2인 막대의 인덱스를 push한다.
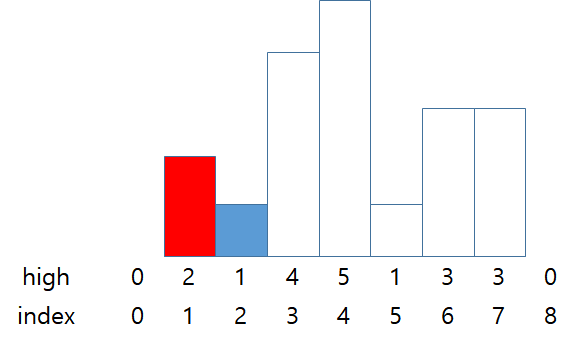
stack = {0, 2}
answer = 2 * 1 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 2의 막대가 더 짧기 때문에 인덱스 2의 막대보다 짧거나 같은 막대가 나올 때까지 스택을 pop하면서 최대 넓이를 구한다.
이후 인덱스 2인 막대의 인덱스를 스택에 푸시한다.
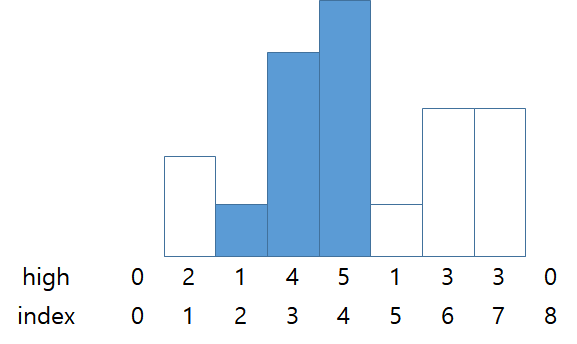
stack = {0, 2, 3, 4}
스택의 가장 위에 있는 막대보다 짧은 막대가 나오기 전까지 스택에 push한다.
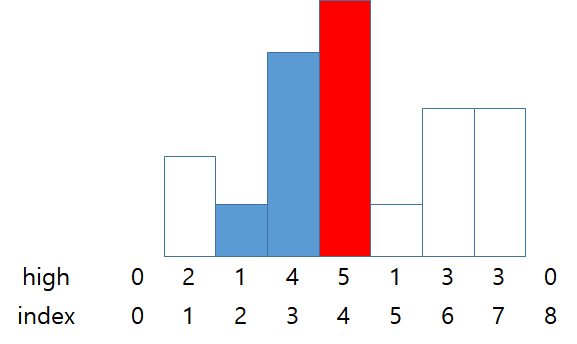
stack = {0, 2, 3}
answer = 5 * 1 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 5의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
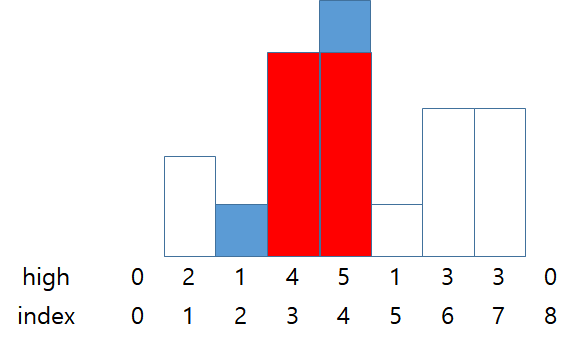
stack = {0, 2}
answer = 4 * 2 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 5의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
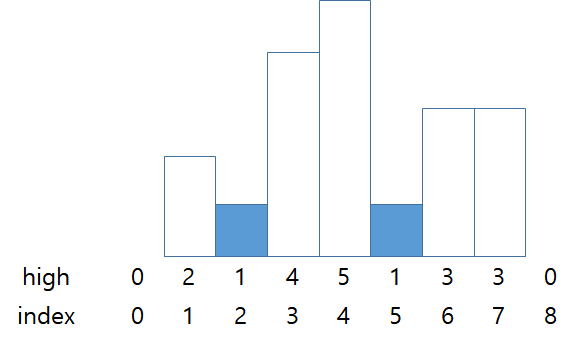
stack = {0, 2, 5}
스택의 가장 위에 있는 막대와 인덱스 5의 막대의 높이가 같기 때문에 스택에 인덱스 5인 막대의 인덱스를 push한다.
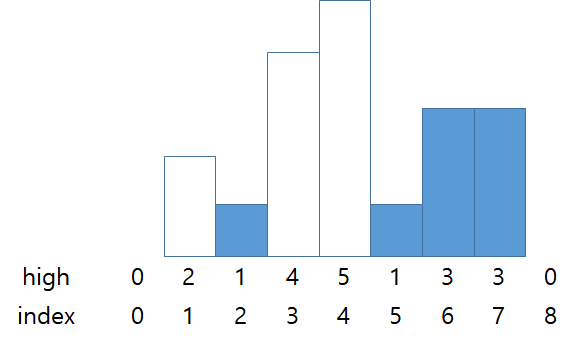
stack = {0, 2, 5, 6, 7}
스택의 가장 위에 있는 막대보다 짧은 막대가 나오기 전까지 스택에 push한다.
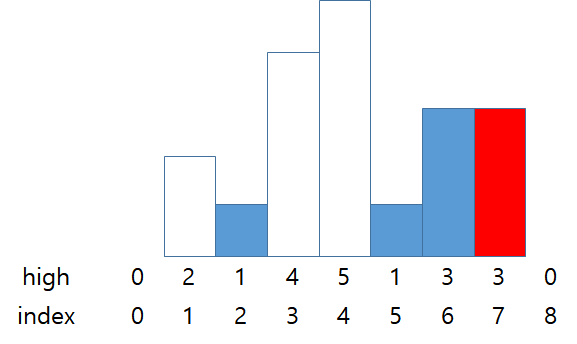
stack = {0, 2, 5, 6}
answer = 3 * 1 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 8의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
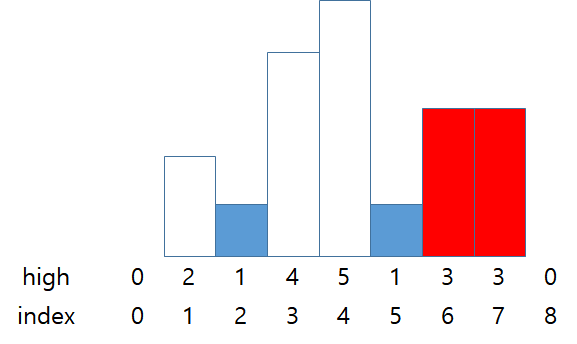
stack = {0, 2, 5}
answer = 3 * 2 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 8의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
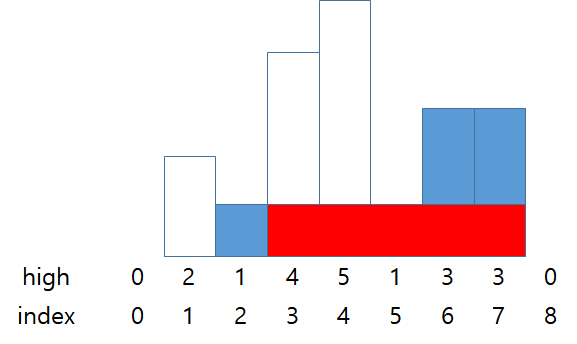
stack = {0, 2}
answer = 1 * 5 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 8의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
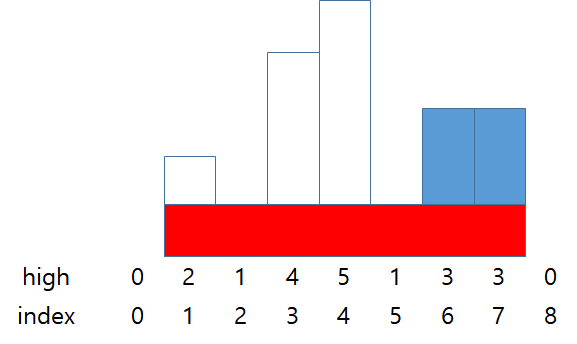
stack = {0}
answer = 1 * 7 (high * width)
스택의 가장 위에 있는 막대보다 인덱스 8의 막대가 더 짧기 때문에 스택의 가장 위의 막대를 pop하고 넓이를 구한다.
코드
import java.util.*
import kotlin.math.*
fun main()= with(System.out.bufferedWriter()){
val br = System.`in`.bufferedReader()
val n = Integer.parseInt(br.readLine())
val high = IntArray(n+2)
val stk = Stack<Int>()
var answer =0
var num:Int
stk.push(0)
for(i in 1 .. n+1){
if(i==n+1){
num=0
}
else {
num = Integer.parseInt(br.readLine())
}
high[i] = num
while(stk.isNotEmpty() && high[stk.peek()]>num){
val highIdx = stk.pop()
answer = max(answer,high[highIdx]*(i-stk.peek()-1))
}
stk.push(i)
}
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2003 수들의 합 2 c++, Kotlin (투 포인터) (0) | 2021.08.27 |
|---|---|
| 백준 6549 히스토그램에서 가장 큰 직사각형 Kotlin (스택) (0) | 2021.08.26 |
| 백준 1238 파티 Kotlin (다익스트라) (0) | 2021.08.21 |
| 백준 16954 움직이는 미로 탈출 c++,Kotlin (bfs) (0) | 2021.08.20 |
| 백준 5214 환승 Kotlin (bfs) (0) | 2021.08.20 |




댓글