문제 출처 : https://www.acmicpc.net/problem/17472
17472번: 다리 만들기 2
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
www.acmicpc.net

문제
섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.
섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.
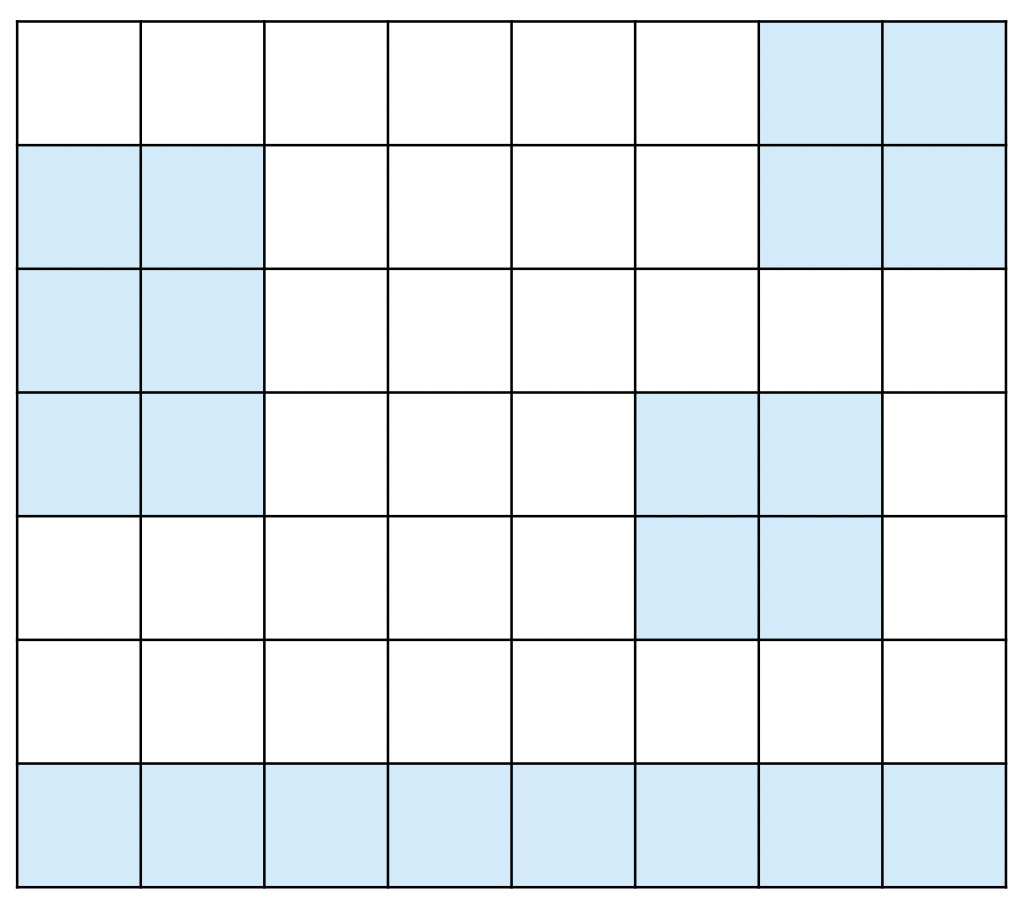
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.
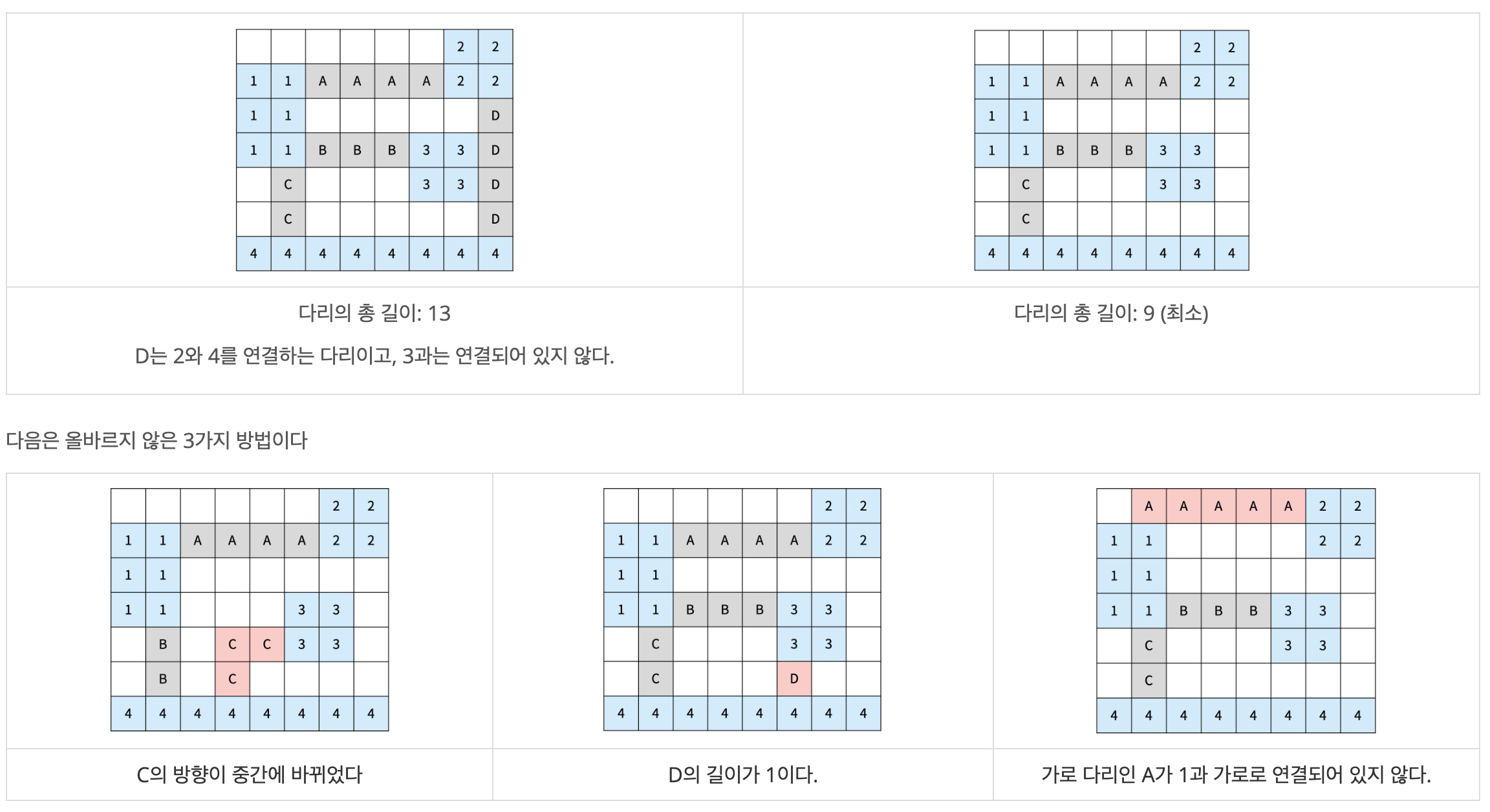
다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다. 아래는 다리가 교차하는 경우와 기타 다른 경우에 대한 2가지 예시이다.
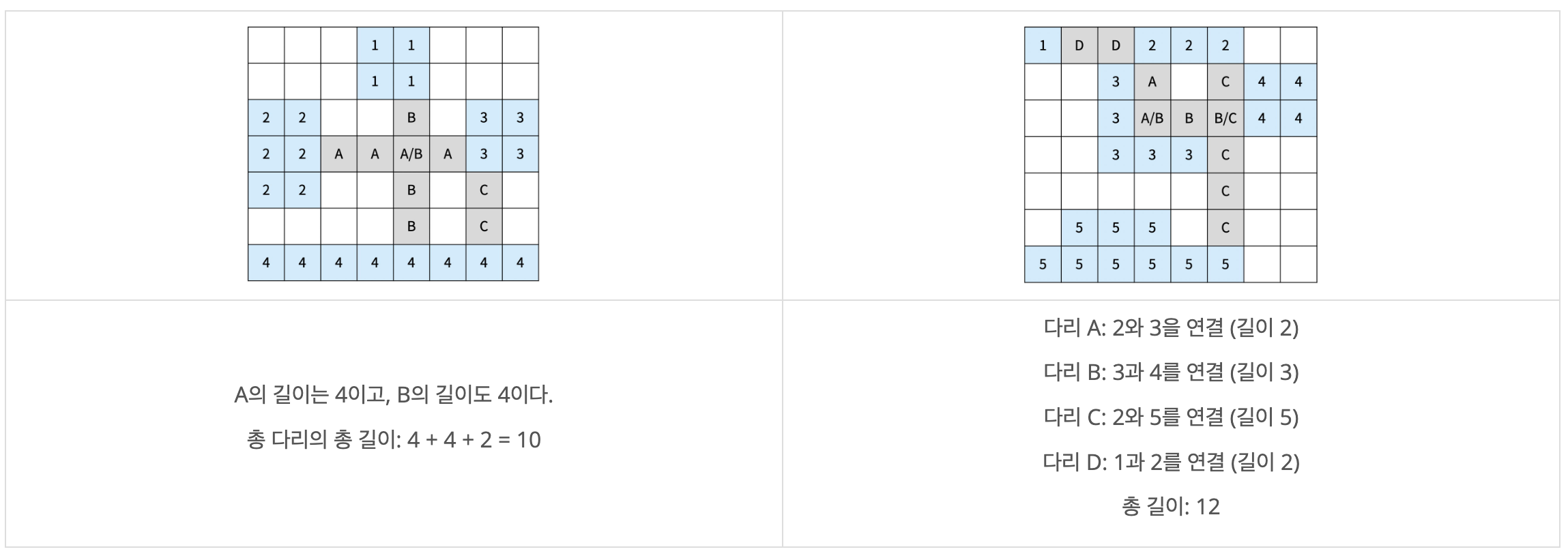
나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
제한
- 1 ≤ N, M ≤ 10
- 3 ≤ N×M ≤ 100
- 2 ≤ 섬의 개수 ≤ 6


풀이
bfs + 크루스칼로 풀 수 있는 아주 좋은 문제~!
이 문제를 건드리는 사람은 bfs는 자유자재로 다룰 수 있고, 적어도 최소 스패닝 트리에 대해 알 것이라 생각한다.
전체적인 풀이는 다음과 같다.
1. 섬을 그룹핑 한다.
2. 그룹핑한 각 섬에서 다른 섬으로 다리를 놓는다. 이때 문제의 조건에 맞게 유효한 다리만 놓아준다.
3. 다리를 놓는다는 것은 어떠한 섬(from)에서 어떠한 섬(to)이 연결되는 간선이 생긴 것이다. 그리고 이 간선엔 다리의 길이(가중치)가 있다.
4. 우리는 모든 섬을 연결하는 데에(사이클 형성) 사용한 다리의 길이의 합이 최솟값이어야 한다.(최소 스패닝 트리) 위에서 구한 간선들로 크루스칼 알고리즘을 돌리자.
크루스칼까지 돌리고 나면 우리가 뽑은 간선을 모두 사용해 섬이 이어져있는 상태이다.
따라서 모든 섬이 이어져있는지 확인하고, 이어져있다면 답을 출력, 이어져있지 않다면 이 간선들을 이용해서 섬을 모두 연결할 수 없다는 의미로 -1을 출력한다.
코드
import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
/*
* 1. 섬 그룹핑하기
* 2. 각 섬에서 다리 놓아보기 (크루스칼에 쓰일 간선)
* 3. 크루스칼 돌리기
* */
data class Edge(
val from: Int,
val to: Int,
val dis: Int
)
val dir = arrayOf(
arrayOf(0, 1),
arrayOf(1, 0),
arrayOf(0, -1),
arrayOf(-1, 0)
)
lateinit var graph: Array<IntArray>
lateinit var visited: Array<BooleanArray>
lateinit var parent: IntArray
val pq = ArrayList<Edge>()
//val pq = PriorityQueue<Edge> { a, b ->
// when {
// a.dis < b.dis -> -1
// a.dis > b.dis -> 1
// else -> 0
// }
//}
fun getParent(x: Int): Int = if(x == parent[x]) x else getParent(parent[x]).also{ parent[x] = it }
fun unionParent(x: Int, y: Int){
val xx = getParent(x)
val yy = getParent(y)
if(xx<yy) parent[yy] = xx
else parent[xx] = yy
}
fun findParent(x: Int, y: Int): Boolean{
val xx = getParent(x)
val yy = getParent(y)
return xx == yy
}
fun setBridge(n: Int, m: Int, r: Int, c: Int) {
for (i in 0 until 4) {
var nr = r+dir[i][0]
var nc = c+dir[i][1]
while (nr in 0 until n && nc in 0 until m && graph[nr][nc] == 0) {
nr += dir[i][0]
nc += dir[i][1]
}
if (nr !in 0 until n || nc !in 0 until m) continue //연결할 섬이 없는 경우
if (graph[r][c] == graph[nr][nc]) continue // 같은 섬에 연결된 경우
val dis = Math.abs(nr - r + nc - c)-1 //둘 중 하나는 0
if (dis <= 1) continue //다리 길이가 1이하인 경우
pq.add(Edge(graph[r][c], graph[nr][nc], dis))
}
}
fun grouping(n: Int, m: Int, r: Int, c: Int, num: Int) {
val q: Queue<Pair<Int, Int>> = LinkedList()
q.add(Pair(r, c))
graph[r][c] = num
while (q.isNotEmpty()) {
val (cr, cc) = q.poll()
for (i in 0 until 4) {
val nr = cr + dir[i][0]
val nc = cc + dir[i][1]
if (nr !in 0 until n || nc !in 0 until m) continue
if (visited[nr][nc]) continue
if (graph[nr][nc] != 1) continue
graph[nr][nc] = num
q.add(Pair(nr, nc))
}
}
}
fun main() = with(System.out.bufferedWriter()) {
//input
val (n, m) = getIntList()
graph = Array(n) { getIntList().toIntArray() }
visited = Array(n) { BooleanArray(m) }
//solve
//grouping
var num = 2
for (r in 0 until n) {
for (c in 0 until m) {
if (graph[r][c] != 1) continue
grouping(n, m, r, c, num++)
}
}
//setBridge
for (r in 0 until n) {
for (c in 0 until m) {
if (graph[r][c] == 0) continue
setBridge(n, m,r,c)
}
}
//Kruskal (섬 연결)
pq.sortBy { it.dis }
parent = IntArray(num){it}
var answer=0
for(edge in pq){
if(!findParent(edge.from, edge.to)){
answer+=edge.dis
unionParent(edge.from,edge.to)
}
}
//output
val p = getParent(2)
for(i in 2 until num){
if(p!= getParent(i)){
write("-1")
close()
return
}
}
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 13335 트럭 Kotlin (구현) (0) | 2022.06.14 |
|---|---|
| 백준 16935 배열 돌리기 3 Kotlin (구현) (0) | 2022.06.13 |
| 백준 17281 ⚾ Kotlin (구현) (0) | 2022.06.11 |
| 백준 16719 ZOAC Kotlin (구현, next_permutation) (0) | 2022.06.10 |
| 백준 20164 홀수 홀릭 호석 Kotlin (완전 탐색) (0) | 2022.06.09 |




댓글