문제 출처 : programmers.co.kr/learn/courses/30/lessons/67260
코딩테스트 연습 - 동굴 탐험
9 [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] [[8,5],[6,7],[4,1]] true 9 [[8,1],[0,1],[1,2],[0,7],[4,7],[0,3],[7,5],[3,6]] [[4,1],[5,2]] true 9 [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] [[4,1],[8,7],[6,5]] false
programmers.co.kr
문제 설명
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]

오지 탐험가인 프로도는 탐험 도중 n개의 방으로 이루어진 지하 동굴을 탐험하게 되었습니다. 모든 방에는 0부터 n - 1 까지 번호가 붙어있고, 이 동굴에 들어갈 수 있는 유일한 입구는 0번 방과 연결되어 있습니다. 각 방들은 양방향으로 통행이 가능한 통로로 서로 연결되어 있는데, 서로 다른 두 방을 직접 연결하는 통로는 오직 하나입니다. 임의의 서로 다른 두 방 사이의 최단경로는 딱 한 가지만 있으며, 또한 임의의 두 방 사이에 이동이 불가능한 경우는 없습니다.
탐험에 앞서 이 지하 동굴의 지도를 손에 넣은 프로도는 다음과 같이 탐험 계획을 세웠습니다.
- 모든 방을 적어도 한 번은 방문해야 합니다.
- 특정 방은 방문하기 전에 반드시 먼저 방문할 방이 정해져 있습니다.
2-1. 이는 A번 방은 방문하기 전에 반드시 B번 방을 먼저 방문해야 한다는 의미입니다.
2-2. 어떤 방을 방문하기 위해 반드시 먼저 방문해야 하는 방은 없거나 또는 1개 입니다.
2-3. 서로 다른 두 개 이상의 방에 대해 먼저 방문해야 하는 방이 같은 경우는 없습니다.
2-4. 어떤 방이 먼저 방문해야 하는 방이면서 동시에 나중에 방문해야 되는 방인 경우는 없습니다.
위 계획 중 2-2, 2-3, 2-4는 순서를 지켜 방문해야 하는 두 방의 쌍이 A → B(A를 먼저 방문하고 B를 방문함) 형태로 유일함을 의미합니다. 즉, 프로도는 아래와 같은 형태로 방문순서가 잡히지 않도록 방문 계획을 세웠습니다.
- A → B, A → C (방문순서 배열 order = [...,[A,B],...,[A,C],...]) 형태로 A를 방문 후에 방문해야 할 방이 B와 C로 두 개 또는 그 이상인 경우
- X → A, Z → A (방문순서 배열 order = [...,[X,A],...,[Z,A],...]) 형태로 A를 방문하기 전에 방문해야 할 방이 X와 Z로 두 개 또는 그 이상 인 경우
- A → B → C (방문순서 배열 order = [...,[A,B],...,[B,C],...) 형태로 B처럼 A 방문 후이면서 동시에 C 방문 전인 경우
그리고 먼저 방문해야 할 방과 나중에 방문할 방을 반드시 연속해서 방문해야 할 필요는 없어 A방을 방문한 후 다른 방을 방문한 후 B방을 방문해도 좋습니다.
방 개수 n, 동굴의 각 통로들이 연결하는 두 방의 번호가 담긴 2차원 배열 path, 프로도가 정한 방문 순서가 담긴 2차원 배열 order가 매개변수로 주어질 때, 프로도가 규칙에 맞게 모든 방을 탐험할 수 있을 지 return 하도록 solution 함수를 완성해주세요.
[제한사항]
- n은 2 이상 200,000 이하입니다.
- path 배열의 세로(행) 길이는 n - 1 입니다.
- path 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
- 두 방 A, B사이를 연결하는 통로를 나타냅니다.
- 통로가 연결하는 두 방 번호가 순서없이 들어있음에 주의하세요.
- order 배열의 세로(행) 길이는 1 이상 (n / 2) 이하입니다.
- order 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
- A번 방을 먼저 방문한 후 B번 방을 방문해야 함을 나타냅니다.
입출력 예
n path order result
| 9 | [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] | [[8,5],[6,7],[4,1]] | true |
| 9 | [[8,1],[0,1],[1,2],[0,7],[4,7],[0,3],[7,5],[3,6]] | [[4,1],[5,2]] | true |
| 9 | [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] | [[4,1],[8,7],[6,5]] | false |
입출력 예에 대한 설명
입출력 예 #1
동굴 그림은 아래와 같습니다.
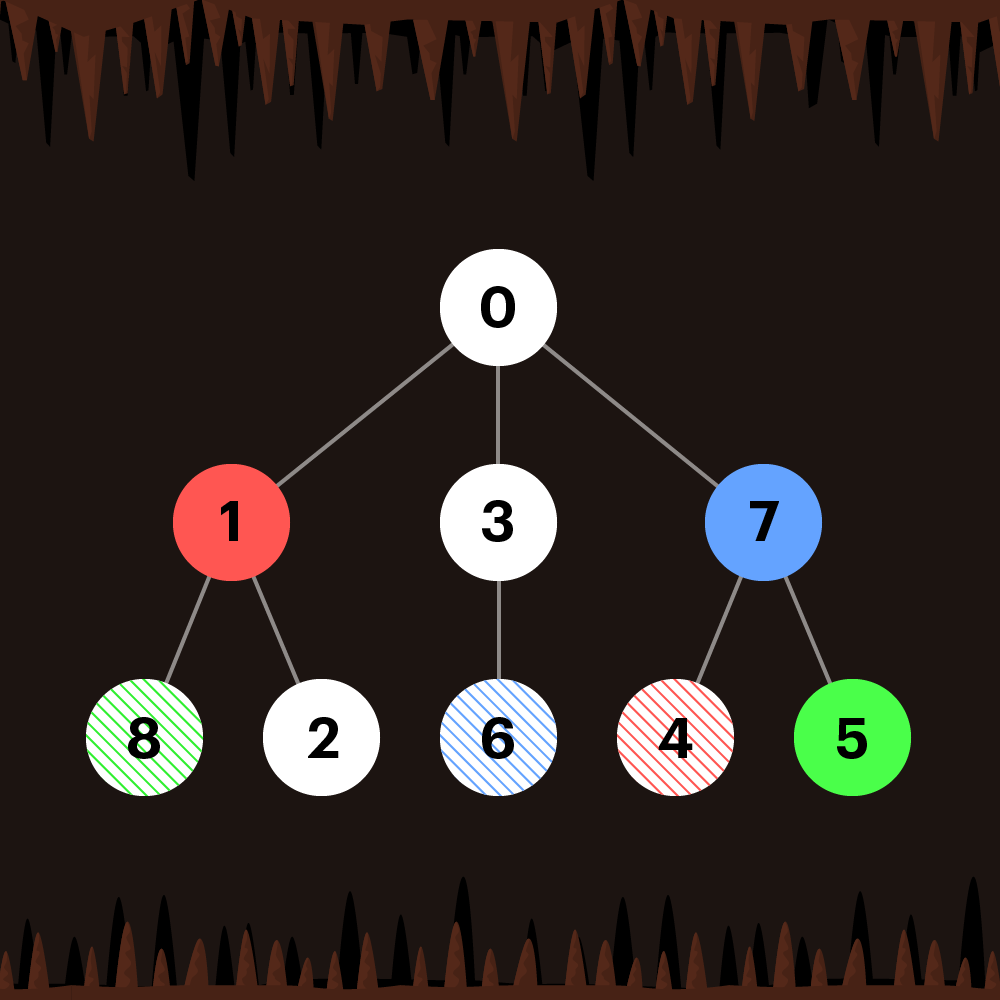
방문 순서를 지켜야 하는 방 번호는 다음과 같습니다.
- 6번 → 7번
- 4번 → 1번
- 8번 → 5번
따라서 모든 방을 방문할 수 있는 방법 중 하나는 다음과 같습니다.
- 0번 → 3번 → 6번 → 3번 → 0번 → 7번 → 4번 → 7번 → 0번 → 1번 → 8번 → 1번 → 2번 → 1번 → 0번 → 7번 → 5번
입출력 예 #2

다음 순서로 각 방을 방문하면 됩니다.
- 0번 → 7번 → 4번 → 7번 → 5번 → 7번 → 0번 → 3번 → 6번 → 3번 → 0번 → 1번 → 8번 → 1번 → 2번
입출력 예 #3
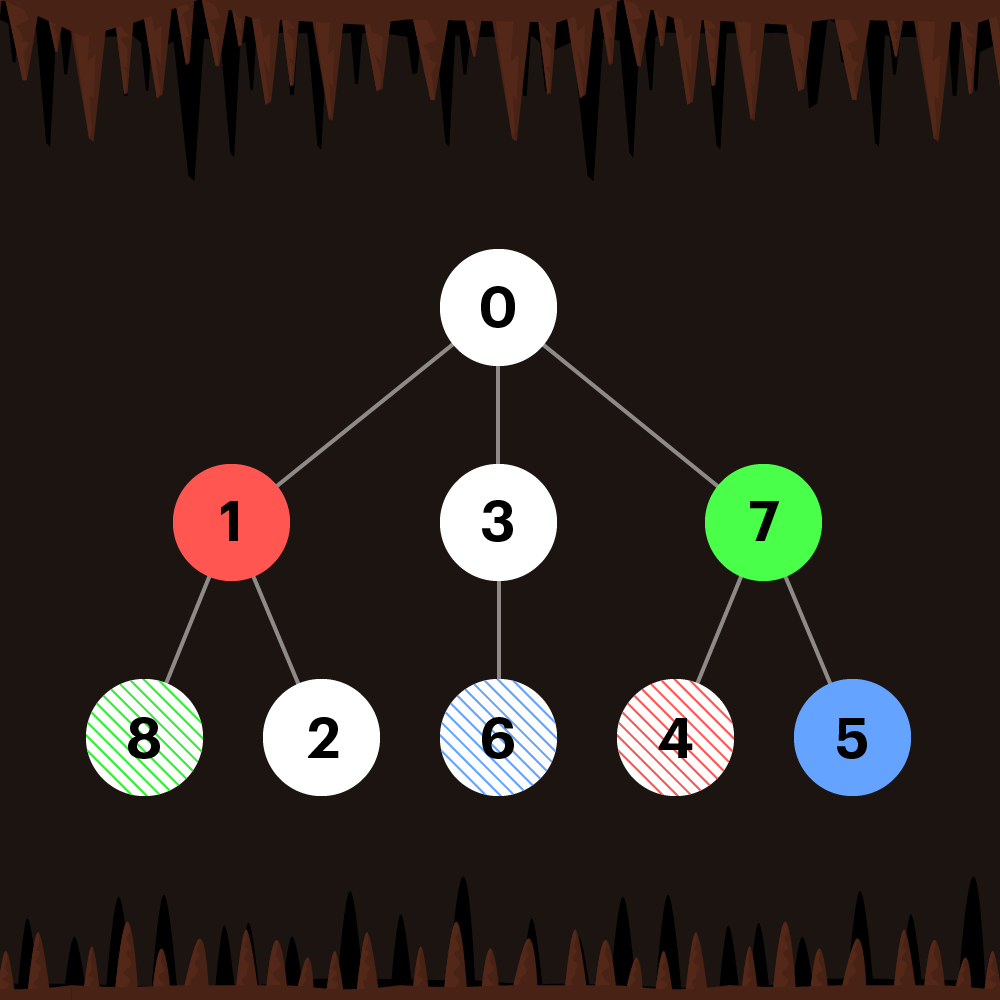
규칙에 맞게 모든 방을 방문할 수 있는 방법이 없습니다.
풀이
5.8일 2021 카카오 인턴십 코딩테스트,
5.9일 프로그래머스 썸머 인턴십 코딩테스트
준비중입니다ㅜ 풀이는 다음 주에 올리겠습니다.
참고 링크
tech.kakao.com/2020/07/01/2020-internship-test/
hy38.github.io/finding-cycles-in-graph
코드
#include <cstring>
#include <vector>
#include <iostream>
#include <queue>
#define MAX 200000
using namespace std;
vector<int> bothway_graph[MAX];
vector<int> oneway_graph[MAX];
bool visited[MAX];
bool finished[MAX];
bool noneCycle=true;
void dfs(int start){
if(noneCycle == false) return;
visited[start]=true;
for(auto next : oneway_graph[start]){
if(!visited[next]){
dfs(next);
}
else if(!finished[next]){
noneCycle= false;
return;
}
}
finished[start] = true;
return;
}
bool solution(int n, vector<vector<int>> path, vector<vector<int>> order) {
for(int i=0; i<path.size();i++){
bothway_graph[path[i][0]].push_back(path[i][1]);
bothway_graph[path[i][1]].push_back(path[i][0]);
}
queue<int> q;
q.push(0);
visited[0]=true;
while(!q.empty()){
int a= q.front();
q.pop();
for(auto i : bothway_graph[a]){
if(!visited[i]){
oneway_graph[a].push_back(i);
visited[i]=true;
q.push(i);
}
}
}
for(auto o : order){
if(o[1]==0)
return false;
oneway_graph[o[0]].push_back(o[1]);
}
memset(visited,0,sizeof(visited));
dfs(0);
// for(int i=0; i<n;i++){
// cout<<"i = "<<i<<": ";
// for(auto o : oneway_graph[i]){
// cout <<o<<' ';
// }
// cout <<'\n';
// }
return noneCycle;
}'알고리즘 문제 풀이 > 프로그래머스' 카테고리의 다른 글
| 2019 카카오 개발자 겨울 인턴십 코딩테스트 튜플 c++ (0) | 2021.05.07 |
|---|---|
| 2019 카카오 개발자 겨울 인턴십 코딩테스트 크레인 인형뽑기 게임 c++ (0) | 2021.05.07 |
| 2020 카카오 인턴십 코딩테스트 문제 보석 쇼핑 c++ (0) | 2021.05.03 |
| 2020 카카오 인턴십 코딩테스트 문제 수식 최대화 c++, Kotlin (순열, 구현) 2022-06-24 코틀린 추가 (0) | 2021.05.02 |
| 2020 카카오 인턴십 코딩테스트 문제 키패드 누르기 c++ (0) | 2021.04.30 |

댓글