문제 출처 : https://www.acmicpc.net/problem/18232
18232번: 텔레포트 정거장
첫 번째 줄에 정수 N, M이 공백으로 구분되어 주어진다. (2 ≤ N ≤ 300,000, 0 ≤ M ≤ min(N×(N-1)/2, 300,000)) 두 번째 줄에 정수 S, E가 공백으로 구분되어 주어진다. (1 ≤ S, E ≤ N, S ≠ E) 그 다음 줄부터 M
www.acmicpc.net

문제
꽉꽉나라에 사는 주예와 방주는 점 S에서 만나 저녁을 먹기로 했다. 주예는 점 S에 도착했지만 길치인 방주가 약속시간이 30분이 지나도 나타나지 않자 방주에게 연락을 하여 방주가 점 E에 있다는 사실을 알아냈다. 주예는 방주에게 그 위치에 가만히 있으라고 했고, 직접 점 E로 가려고 한다.
꽉꽉나라에는 1부터 N까지의 각 점에 하나의 텔레포트 정거장이 위치해 있고 텔레포트를 통하여 연결되어 있는 다른 텔레포트의 정거장으로 이동할 수 있다. 주예는 현재 위치가 점 X라면 X+1이나 X-1로 이동하거나 X에 위치한 텔레포트와 연결된 지점으로 이동할 수 있으며 각 행동에는 1초가 소요된다. 배가 고픈 주예는 최대한 빨리 방주와 만나고 싶어 한다.
N과 텔레포트 연결 정보가 주어질 때 점 S에 있는 주예가 점 E까지 가는 최소 시간을 구해보자.
입력
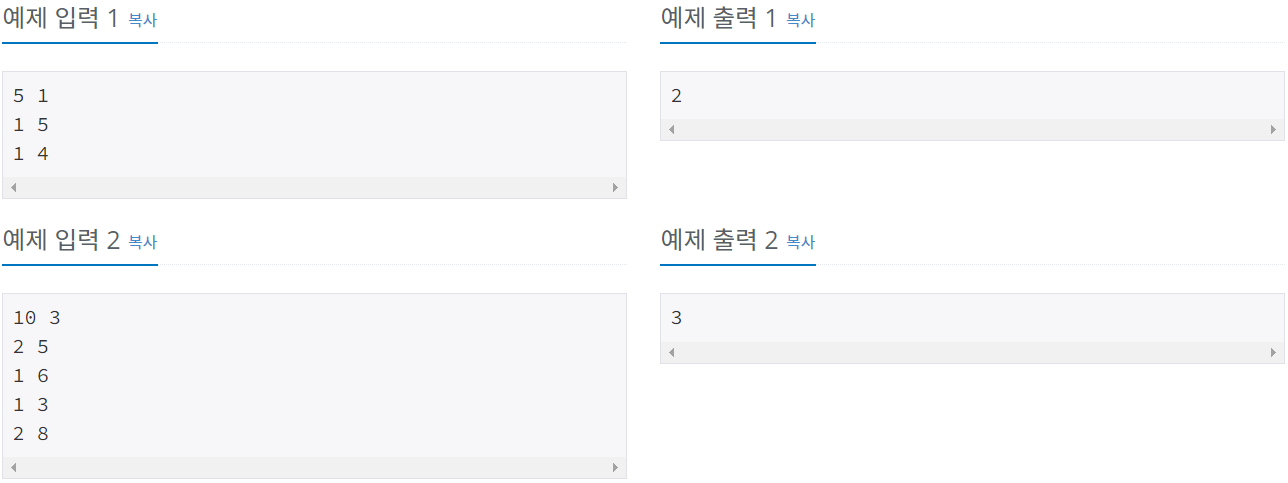
첫 번째 줄에 정수 N, M이 공백으로 구분되어 주어진다. (2 ≤ N ≤ 300,000, 0 ≤ M ≤ min(N×(N-1)/2, 300,000))
두 번째 줄에 정수 S, E가 공백으로 구분되어 주어진다. (1 ≤ S, E ≤ N, S ≠ E)
그 다음 줄부터 M개의 줄에 걸쳐 텔레포트 연결 정보를 의미하는 정수 x, y가 주어진다. (1 ≤ x, y ≤ N, x ≠ y)
x y는 점 x의 텔레포트와 점 y의 텔레포트가 연결되어 있다는 뜻이다. M개의 연결정보는 중복되는 x y쌍이 없도록 주어진다.
출력
첫 번째 줄에 주예와 방주가 만날 수 있는 최소 시간을 출력한다.
알고리즘 분류
풀이
bfs 문제이다.
dp로도 풀 수 있을 것 같아서
추후에 dp로 리팩토링해볼 예정이다.
일단 그래프 탐색 방향은 1차원 좌표에서 +1, -1, 텔레포트로 3가지이다.
이 세가지 방향으로 일반적인 bfs를 짜면 되는데, 내가 틀렸던 이유는 x와 y모두 중복값이 없다고 생각했기 때문이다.
예를 들어 텔레포트가
1, 4
1, 2
1, 5이면 4도 가고, 2도 가고 5도 가야 하는데 셋 중 하나만 갔다.
이 부분만 유의해서 풀면 쉽게 풀 수 있다.
코드
import java.util.*
val br = System.`in`.bufferedReader()
const val MAX = 3000000
val teleport = Array(MAX+1){ArrayList<Int>()}
val visited = BooleanArray(MAX+1)
fun bfs(s : Int, e : Int, n : Int) : Int{
val q : Queue<Pair<Int,Int>> = LinkedList<Pair<Int,Int>>()
q.add(Pair(s,0))
visited[s]=true
while(q.isNotEmpty()){
val cur = q.poll()
for(next in teleport[cur.first]){
if(visited[next]) continue
if(next==e){
return cur.second+1
}
visited[next]=true
q.add(Pair(next,cur.second+1))
}
for(i in 1 downTo -1 step 2){
val next = cur.first+i
if(next !in 1 .. MAX)continue
if(visited[next]) continue
if(next==e){
return cur.second+1
}
visited[next]=true
q.add(Pair(next,cur.second+1))
}
}
return 0
}
fun main() = with(System.out.bufferedWriter()){
val (n,m) = br.readLine().split(' ').map{it.toInt()}
val (s,e) = br.readLine().split(' ').map{it.toInt()}
for(i in 0 until m){
val (from, to) = br.readLine().split(' ').map{it.toInt()}
teleport[from].add(to)
teleport[to].add(from)
}
write("${bfs(s,e,n)}")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 11663 선분 위의 점 Kotlin (이분 탐색) (0) | 2022.01.22 |
|---|---|
| 백준 2225 합분해 Kotlin (dp) (0) | 2022.01.20 |
| 백준 17136 색종이 붙이기 Kotlin (백트래킹) (0) | 2022.01.18 |
| 백준 12101 1, 2, 3 더하기 2 Kotlin (순열) (0) | 2022.01.17 |
| 백준 11050 이항 계수 1 Kotlin (재귀) (0) | 2022.01.16 |




댓글