문제 출처 : https://www.acmicpc.net/problem/2146
2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다
www.acmicpc.net

문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
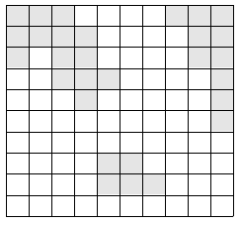
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.
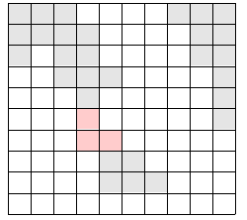
물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.

알고리즘 분류
풀이
쉽게 풀릴 것 같았는데, 생각보다 더 고려해야 할 점이 많았다.
일단 전반적인 풀이는 다음과 같다.
1. 각 섬들을 넘버링한다.
2. 넘버링 된 섬들의 좌표들을 모두 큐에 삽입한다.
3. 매 턴마다 그래프의 상태를 갱신한다.(모든 섬, 모든 좌표를 인접한 칸으로 이동)
4. 이동하면서 dp배열에 이동한 횟수를 저장하고, 큐에도 현재 이동 횟수를 저장한다.
5-1. 다른 섬을 만나는 순간 dp배열의 값과 큐의 현재 이동 횟수를 더한 값 중 최솟값을 출력한다.
5-2. 이때, 더한 값 중 최솟값을 출력하라는 것은, 다른 섬을 만나는 순간 바로 종료하지 않고, 그 턴까진 모두 이동시키고
그 중 최솟값을 찾으란 말이다.
여기 좋은 반례가 있다.
https://www.acmicpc.net/board/view/20484
10002
00000
00000
00000
33004
위와 같은 상태일 때, 위의 좌표부터 큐에서 이동하기 때문에, 3과 4가 만나는 거리인 2가 아닌,
1과 2가 만나는 거리인 3이 나올 수 있다.
매 턴마다 그래프의 상태를 갱신하고, 섬이 만나는 순간 바로 종료하지 않는 이유이다.
(시뮬레이션)
턴 1
11022
10002
00000
30004
33344
턴 2
11122
10002
00000
30004
33344
종료
2022.06.02 내용 추가
다시 풀어봤는데, 이전엔 꽤나 열심히 풀었구나.
아래에 새로운 코드를 추가했다.
이번에 다시 풀었을 땐 메모이제이션 따위 하지 않고 그냥 나이브하게 풀었다.
우선 동일하게 섬들을 넘버링한 후, 모든 섬의 모든 좌표에서 다른 섬으로 가는 최단 거리를 구했다.
메모리는 좀 차이가 나지만, 시간은 136ms정도 밖에 차이 나지 않는다.
만약 코테에서 이런 문제가 나왔을 때, 입력 제한이 크다면 위의 첫 번째 풀이로 풀어야겠지만,
아니라면 두 번째 풀이로 풀 것이다.
통과만 하면 장땡. 바로 다음 문제 풀러 가자.
코드1

import kotlin.math.*
import java.util.*
val dirXY = arrayOf(arrayOf(0,1),arrayOf(0,-1),arrayOf(1,0),arrayOf(-1,0))
val INF = 987654321
val br = System.`in`.bufferedReader()
data class Node(var r : Int, var c : Int,var num : Int, var dis : Int)
var answer = INF
val q : Queue<Node> = LinkedList<Node>()
fun bfs(n : Int, graph : Array<IntArray>){
val dp = Array(n){IntArray(n)}
while(q.isNotEmpty()){
val qSize = q.size
for(i in 0 until qSize) {
val cur = q.poll()
for (j in 0 until 4) {
val nr = cur.r + dirXY[j][0]
val nc = cur.c + dirXY[j][1]
if (nr !in 0 until n || nc !in 0 until n) continue
if (graph[nr][nc] != cur.num && graph[nr][nc] != 0){
answer = min(answer,cur.dis+dp[nr][nc])
}
if (graph[nr][nc] == 0) {
q.add(Node(nr, nc, cur.num, cur.dis + 1))
dp[nr][nc] = cur.dis + 1
graph[nr][nc] = cur.num
}
}
}
if(answer!=INF) return
}
}
fun numbering(i : Int, j : Int,num : Int,n : Int, graph : Array<IntArray>, visited : Array<BooleanArray>){
val qq : Queue<Pair<Int,Int>> = LinkedList<Pair<Int,Int>>()
graph[i][j]=num
visited[i][j]=true
qq.add(Pair(i,j))
while(qq.isNotEmpty()){
val cur = qq.poll()
for(i in 0 until 4){
val nr = cur.first+dirXY[i][0]
val nc = cur.second+dirXY[i][1]
if(nr !in 0 until n || nc !in 0 until n) continue
if(graph[nr][nc]==0 || visited[nr][nc])continue
graph[nr][nc]=num
visited[nr][nc]=true
qq.add(Pair(nr,nc))
q.add(Node(nr,nc,num,0))
}
}
}
fun main() = with(System.out.bufferedWriter()){
val n = br.readLine().toInt()
val graph = Array(n){
br.readLine().split(' ').map{it.toInt()}.toIntArray()
}
var num=1
val visited= Array(n){BooleanArray(n)}
for(i in 0 until n){
for(j in 0 until n){
if(visited[i][j] || graph[i][j]==0) continue
q.add(Node(i,j,num,0))
numbering(i,j,num++,n,graph,visited)
}
}
bfs(n,graph)
write("$answer")
close()
}코드2

import java.util.*
val br = System.`in`.bufferedReader()
fun getIntList() = br.readLine().split(' ').map { it.toInt() }
fun getInt() = br.readLine().toInt()
data class Node(
val r: Int,
val c: Int,
val dis: Int
)
lateinit var graph: Array<IntArray>
lateinit var visited: Array<BooleanArray>
var answer = Int.MAX_VALUE
val dir = arrayOf(
arrayOf(0,1),
arrayOf(1,0),
arrayOf(0,-1),
arrayOf(-1,0)
)
fun bfs(r: Int, c: Int, n: Int, num: Int, type: String){
if(type=="preSet") {
val q: Queue<Pair<Int, Int>> = LinkedList()
q.add(Pair(r, c))
graph[r][c] = num
while (q.isNotEmpty()) {
val (cr, cc) = q.poll()
for (i in 0 until 4) {
val nr = cr + dir[i][0]
val nc = cc + dir[i][1]
if (nr !in 0 until n || nc !in 0 until n) continue
if (graph[nr][nc] == 1) {
q.add(Pair(nr, nc))
graph[nr][nc] = num
}
}
}
}
else{
val q: Queue<Node> = LinkedList()
q.add(Node(r,c,0))
visited[r][c] = true
while(q.isNotEmpty()){
val (cr, cc, cDis) = q.poll()
for(i in 0 until 4){
val nr = cr + dir[i][0]
val nc = cc + dir[i][1]
if(nr !in 0 until n || nc !in 0 until n) continue
if(visited[nr][nc]) continue
if(graph[nr][nc] == num) continue
if(graph[nr][nc] == 0){
q.add(Node(nr,nc,cDis+1))
visited[nr][nc] = true
}
else{
answer = answer.coerceAtMost(cDis)
return
}
}
}
}
}
fun main() = with(System.out.bufferedWriter()){
//input
val n = getInt()
graph = Array(n){ getIntList().toIntArray() }
//solve
var num =2
for(i in 0 until n){
for(j in 0 until n){
if(graph[i][j] == 1) {
bfs(i,j,n,num++, "preSet")
}
}
}
for(i in 0 until n){
for(j in 0 until n){
if(graph[i][j]!=0) {
visited = Array(n) { BooleanArray(n)}
bfs(i,j,n,graph[i][j],"solve")
}
}
}
//output
write("$answer")
close()
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 2331 반복수열 Kotlin (dfs) (0) | 2021.12.20 |
|---|---|
| 백준 1525 퍼즐 Kotlin (bfs) (0) | 2021.12.20 |
| 백준 3055 탈출 Kotlin (bfs) (0) | 2021.12.19 |
| 백준 1749 점수따먹기 Kotlin (2차원 누적 합) (0) | 2021.12.18 |
| 백준 1726 로봇 Kotlin (bfs) 2022-06-15 다익스트라 추가 (0) | 2021.12.17 |




댓글