문제 출처 : https://www.acmicpc.net/problem/16234
16234번: 인구 이동
N×N크기의 땅이 있고, 땅은 1×1개의 칸으로 나누어져 있다. 각각의 땅에는 나라가 하나씩 존재하며, r행 c열에 있는 나라에는 A[r][c]명이 살고 있다. 인접한 나라 사이에는 국경선이 존재한다. 모
www.acmicpc.net
문제
N×N크기의 땅이 있고, 땅은 1×1개의 칸으로 나누어져 있다. 각각의 땅에는 나라가 하나씩 존재하며, r행 c열에 있는 나라에는 A[r][c]명이 살고 있다. 인접한 나라 사이에는 국경선이 존재한다. 모든 나라는 1×1 크기이기 때문에, 모든 국경선은 정사각형 형태이다.
오늘부터 인구 이동이 시작되는 날이다.
인구 이동은 하루 동안 다음과 같이 진행되고, 더 이상 아래 방법에 의해 인구 이동이 없을 때까지 지속된다.
- 국경선을 공유하는 두 나라의 인구 차이가 L명 이상, R명 이하라면, 두 나라가 공유하는 국경선을 오늘 하루 동안 연다.
- 위의 조건에 의해 열어야하는 국경선이 모두 열렸다면, 인구 이동을 시작한다.
- 국경선이 열려있어 인접한 칸만을 이용해 이동할 수 있으면, 그 나라를 오늘 하루 동안은 연합이라고 한다.
- 연합을 이루고 있는 각 칸의 인구수는 (연합의 인구수) / (연합을 이루고 있는 칸의 개수)가 된다. 편의상 소수점은 버린다.
- 연합을 해체하고, 모든 국경선을 닫는다.
각 나라의 인구수가 주어졌을 때, 인구 이동이 며칠 동안 발생하는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N, L, R이 주어진다. (1 ≤ N ≤ 50, 1 ≤ L ≤ R ≤ 100)
둘째 줄부터 N개의 줄에 각 나라의 인구수가 주어진다. r행 c열에 주어지는 정수는 A[r][c]의 값이다. (0 ≤ A[r][c] ≤ 100)
인구 이동이 발생하는 일수가 2,000번 보다 작거나 같은 입력만 주어진다.
출력
인구 이동이 며칠 동안 발생하는지 첫째 줄에 출력한다.

초기 상태는 아래와 같다.
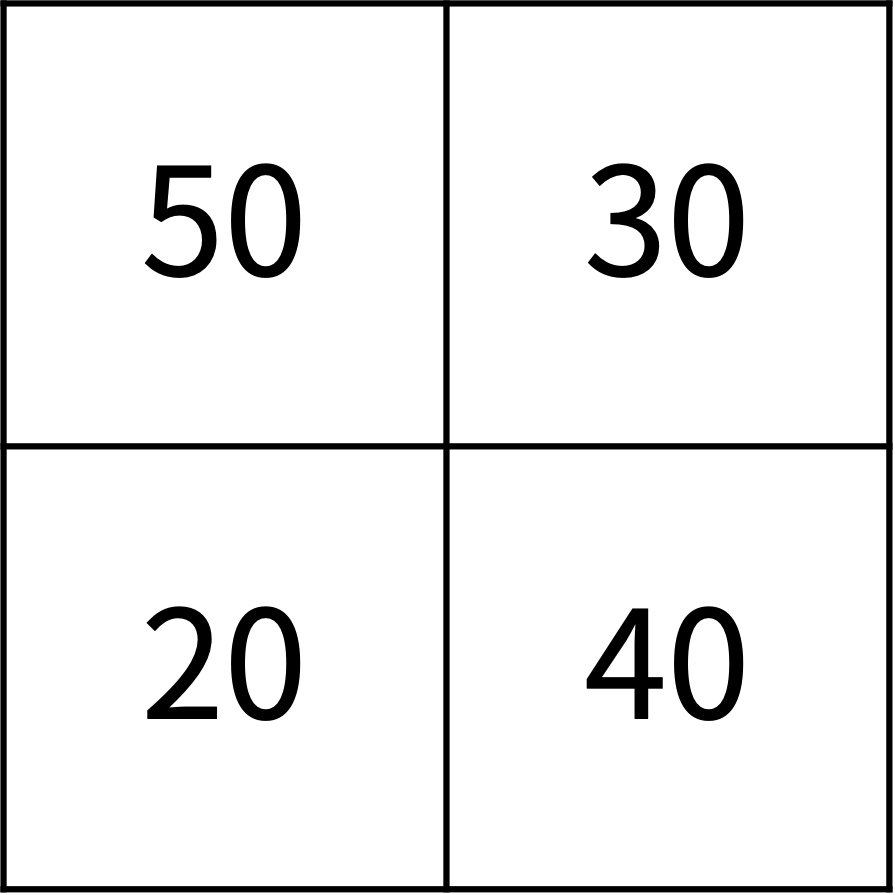
L = 20, R = 50 이기 때문에, 모든 나라 사이의 국경선이 열린다. (열린 국경선은 점선으로 표시)

연합은 하나 존재하고, 연합의 인구는 (50 + 30 + 20 + 40) 이다. 연합의 크기가 4이기 때문에, 각 칸의 인구수는 140/4 = 35명이 되어야 한다.


경계를 공유하는 나라의 인구 차이가 모두 L보다 작아서 인구 이동이 발생하지 않는다.

초기 상태는 아래와 같다.

L = 20, R = 50이기 때문에, 아래와 같이 국경선이 열린다.

인구 수는 합쳐져있는 연합의 인구수는 (50+30+30) / 3 = 36 (소수점 버림)이 되어야 한다.


알고리즘 분류
풀이
우선 bfs 혹은 dfs로 인접한 나라에 인구 이동(연합)이 가능한지 확인해야 하는 것은 쉽게 알 수 있다.
따라서 그래프의 모든 나라에 대해, 인접한 나라와 연합이 가능한지 bfs로 확인하고, 한 번이라도
연합이 있었다면 그 하루는 인구 이동이 있었기 때문에 결과를 +1 해준다.
인구 이동이 가능한 나라를 찾으면 바로 인구 이동을 수행하되, 하루에 연합은 여러 개 있을 수 있기 때문에,
인구 이동한 그래프를 따로 저장해 주고, 하루가 지나면 인구 이동한 그래프를 원래 그래프에 합쳐줘서 하룻동안 여러 개의 연합의 인구 이동을 표현하여 정확한 인구 이동 일 수를 알 수 있다.
코드
#include <iostream>
#include <queue>
#include <cstring>
#include <math.h>
using namespace std;
int n, l, r;
int cnt = 0, people = 0;
int graph[50][50];
int graph_copy[50][50];
bool visited[50][50];
int dir[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };
void cal(vector<pair<int,int>> &coordinate) {
int calPeople = people / cnt;
for (int i = 0; i < coordinate.size(); i++) {
graph_copy[coordinate[i].first][coordinate[i].second] = calPeople;
}
}
vector<pair<int, int>> bfs(int x, int y) {
queue<pair<int, int>> q;
q.push({ x,y });
vector<pair<int, int>> coordinate;
visited[x][y] = true;
while (!q.empty()) {
int cr = q.front().first;
int cc = q.front().second;
q.pop();
coordinate.push_back({ cr,cc });
cnt++;
people += graph[cr][cc];
for (int i = 0; i < 4; i++) {
int nr = cr + dir[i][0];
int nc = cc + dir[i][1];
if (nr >= 0 && nr < n && nc >= 0 && nc < n && !visited[nr][nc]) {
int dif = abs(graph[nr][nc] - graph[cr][cc]);
if (dif >= l && dif <= r) {
q.push({ nr,nc });
visited[nr][nc] = true;
}
}
}
}
return coordinate;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> l >> r;
bool isFinished = false;
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> graph_copy[i][j];
}
}
while (!isFinished) {
isFinished = true;
//bfs첨부터 끝까지 탐색
copy(&graph_copy[0][0], &graph_copy[0][0] + 2500, &graph[0][0]);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//solve
vector<pair<int, int>> coordinate(bfs(i, j));
if (coordinate.size()>1) {
isFinished = false;
//cal
cal(coordinate);
}
//reset
memset(visited, false, sizeof(visited));
cnt = 0;
people = 0;
}
}
if (!isFinished)
result++;
}
cout << result;
return 0;
}'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 7569 토마토 c++ (bfs) (0) | 2021.07.29 |
|---|---|
| 백준 2636 치즈 c++ (bfs) (0) | 2021.07.28 |
| 백준 5427 불 c++ (bf) (0) | 2021.07.27 |
| 백준 5547 일루미네이션 c++ (bfs) 2022-07-06 Kotlin 추가 (0) | 2021.07.27 |
| 백준 4179 불! c++(bfs) (0) | 2021.07.26 |




댓글