문제 출처 : https://www.acmicpc.net/problem/1038
1038번: 감소하는 수
음이 아닌 정수 X의 자릿수가 가장 큰 자릿수부터 작은 자릿수까지 감소한다면, 그 수를 감소하는 수라고 한다. 예를 들어, 321과 950은 감소하는 수지만, 322와 958은 아니다. N번째 감소하는 수를
www.acmicpc.net

문제
음이 아닌 정수 X의 자릿수가 가장 큰 자릿수부터 작은 자릿수까지 감소한다면, 그 수를 감소하는 수라고 한다. 예를 들어, 321과 950은 감소하는 수지만, 322와 958은 아니다. N번째 감소하는 수를 출력하는 프로그램을 작성하시오. 0은 0번째 감소하는 수이고, 1은 1번째 감소하는 수이다. 만약 N번째 감소하는 수가 없다면 -1을 출력한다.
입력
첫째 줄에 N이 주어진다. N은 1,000,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄에 N번째 감소하는 수를 출력한다.

알고리즘 분류
풀이
이 문제는 무작정 완전 탐색으로 풀면 시간 초과가 뜬다.
따라서 컴퓨터에게 좀 더 스마트하게 동작하게끔 도와줘야 된다.
우선 컴퓨터의 수행 시간을 줄이기 위해선 규칙을 찾아서, 감소하는 수를 찾는 범위를 줄여줘야 한다.
N의 자릿수가 한 개일 때, N의 맨 앞자리 수가 0~부터 9일 때 가능한 감소하는 수는,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9이다.
이를 N의 자릿수가 한 개이고, N의 맨 앞자리 수가 0~9일 때
각각의 앞 자리수에서 나올 수 있는 감소하는 수의 개수를 표로 나타내면 다음과 같다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
N의 자릿수가 두 개이고, N의 맨 앞자리 수가 1~9일 때는 다음과 같다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
//N의 자릿수가 두 개 이상일 땐, 맨 앞자리 수가 0이 올 수 없다 ex) 04==4, 05==5
//맨 앞 자릿수가 1일 땐 10
//2일 땐 20, 21
//3일 땐 30, 31, 32
//5일 땐 50, 51, 52, 53, 54
N의 자릿수가 세 개이고, N의 맨 앞자리 수가 1~9일 때는 다음과 같다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
이를 2차원 그래프로 만들어보자.
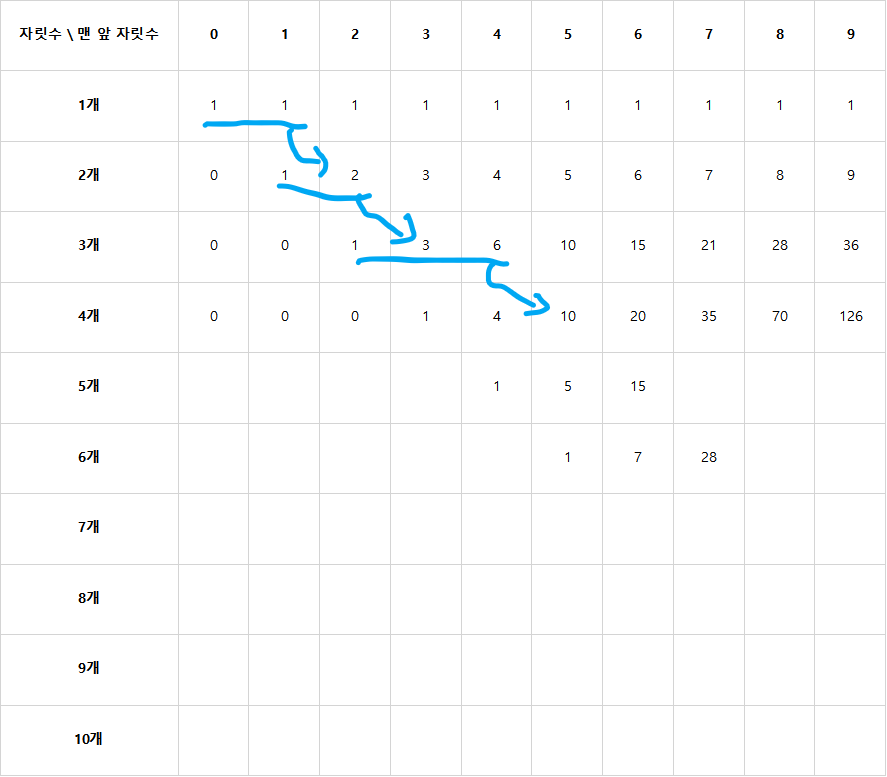
위의 그래프를 보면, N이 i개의 자릿수를 가질 때, 맨 앞 자릿수가 j라고 하면,
(i,j)일 때 가능한 감소하는 수는 (i-1,0)+(i-1,1)+...+(i-1,j-1)라는 걸 알 수 있다.
이 규칙으로 표를 채우면 값은 아래와 같다.

이제 이 그래프를 가지고, 우리는 자릿수가 몇 개(r)인지 알 수 있고, 맨 앞자리 수의 숫자(c)도 알 수 있고,
맨 앞자리 수에서 몇 번째(seq)를 찾아야 하는지도 알 수 있다.
이제 이 재료를 가지고 c로 시작하며 r개의 자릿수를 가지는 조합 중에 seq번째 조합을 찾으면 된다!
코드
#include <iostream>
#include <string>
using namespace std;
int graph[11][10];
int cnt;
int seq;
int r, c;
bool findSeq;
string str;
string ans;
void makeGraph(int num) {
for (int i = 1; i <= 9; i++) {
graph[1][i] = 1;
cnt++;
}
for (int i = 1; i <= 9; i++) {
graph[2][i] = i;
cnt += i;
if (!findSeq&&num <= cnt) {
findSeq = true;
r = 2;
c = i;
seq = cnt - num;
//seq = num - (cnt - graph[2][i]);
}
}
for (int i = 3; i <= 10; i++) {
for (int j = i - 1; j <= 9; j++) {
for (int k = 1; k < j; k++) {
graph[i][j] += graph[i - 1][k];
cnt += graph[i - 1][k];
}
if (!findSeq&&num <= cnt) {
findSeq = true;
r = i;
c = j;
seq = cnt - num;
//seq = num - (cnt - graph[i][j]);
}
}
}
}
void combination() {
if (str.length() == r) {
if (seq-- == 0) {
ans = str;
}
return;
}
for (int i = c; i >= 0; i--) {
if (str[str.length() - 1] - '0' <= i)
continue;
str += (i + '0');
combination();
str.pop_back();
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int num;
cin >> num;
if (num <= 10 ) {//num이 10 이하면 그대로 출력
cout << num;
}
//987654321은 가장 큰 감소하는 수로,1022번째 감소하는 수이다.
//만약 num이 1022보다 크면 감소하는 수를 만들 수 없다.
else if (num > cnt) {
cout << -1;
}
else{
makeGraph(num);
str += c + '0';
combination();
cout << ans << '\n';
}
return 0;
}
'알고리즘 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 1052 물병 c++ (탐욕법) (0) | 2021.07.21 |
|---|---|
| 백준 1041 주사위 c++ (탐욕법) (4) | 2021.07.20 |
| 백준 1025 제곱수 찾기 리뉴얼!! c++, Kotlin (완전 탐색) (0) | 2021.07.18 |
| 백준 1516 게임 개발 c++ (위상 정렬) (0) | 2021.07.16 |
| 백준 1005 ACM Craft c++(위상 정렬) (0) | 2021.07.16 |




댓글