문제 출처 : https://programmers.co.kr/learn/courses/30/lessons/76503
코딩테스트 연습 - 모두 0으로 만들기
각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다. 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한
programmers.co.kr
문제 설명
각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다.
- 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한쪽은 1 감소시킵니다.
하지만, 모든 트리가 위의 행동을 통하여 모든 점들의 가중치를 0으로 만들 수 있는 것은 아닙니다. 당신은 주어진 트리에 대해서 해당 사항이 가능한지 판별하고, 만약 가능하다면 최소한의 행동을 통하여 모든 점들의 가중치를 0으로 만들고자 합니다.
트리의 각 점의 가중치를 의미하는 1차원 정수 배열 a와 트리의 간선 정보를 의미하는 edges가 매개변수로 주어집니다. 주어진 행동을 통해 트리의 모든 점들의 가중치를 0으로 만드는 것이 불가능하다면 -1을, 가능하다면 최소 몇 번만에 가능한지를 찾아 return 하도록 solution 함수를 완성해주세요. (만약 처음부터 트리의 모든 정점의 가중치가 0이라면, 0을 return 해야 합니다.)
제한사항
- a의 길이는 2 이상 300,000 이하입니다.
- a의 모든 수는 각각 -1,000,000 이상 1,000,000 이하입니다.
- a[i]는 i번 정점의 가중치를 의미합니다.
- edges의 행의 개수는 (a의 길이 - 1)입니다.
- edges의 각 행은 [u, v] 2개의 정수로 이루어져 있으며, 이는 u번 정점과 v번 정점이 간선으로 연결되어 있음을 의미합니다.
- edges가 나타내는 그래프는 항상 트리로 주어집니다.
입출력 예
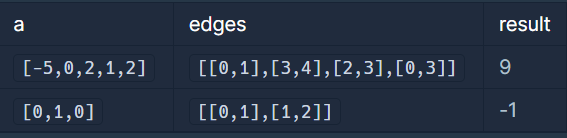
입출력 예 설명
입출력 예 #1
- 다음 그림은 주어진 트리의 모든 정점의 가중치를 0으로 만드는 과정을 나타낸 것입니다.
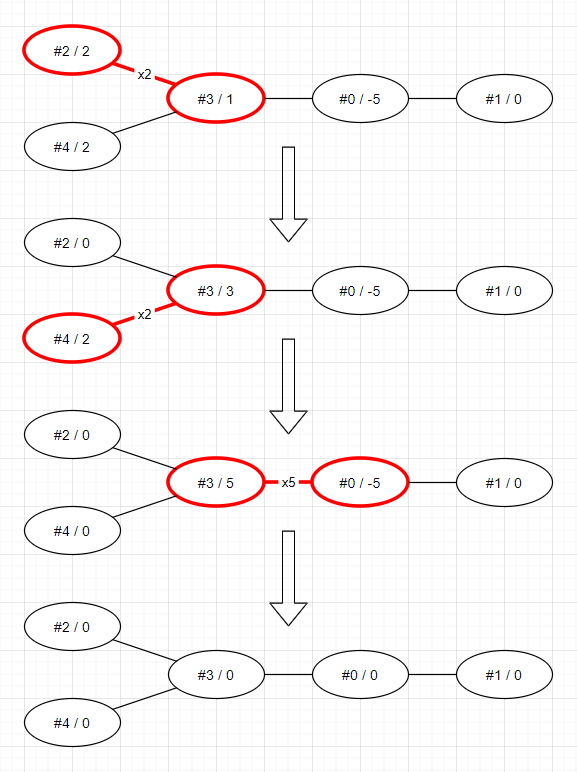
- 2번 정점과 3번 정점을 선택하여 2번 정점은 1 감소시키고, 3번 정점은 1 증가시킵니다. (2번 반복)
- 3번 정점과 4번 정점을 선택하여 4번 정점은 1 감소시키고, 3번 정점은 1 증가시킵니다. (2번 반복)
- 0번 정점과 3번 정점을 선택하여 3번 정점은 1 감소시키고, 0번 정점은 1 증가시킵니다. (5번 반복)
- 모든 정점의 가중치를 0으로 만드는 데 필요한 최소 행동 횟수는 9번이므로, 9를 return 해야 합니다.
입출력 예 #2
- 주어진 트리는 모든 정점의 가중치를 0으로 만드는 것이 불가능하므로, -1을 return 해야 합니다.
풀이
'프로그래머스 / 월간 코드 챌린지 시즌2 / 모두 0으로 만들기'로 분류되어 있는 문제이다.
주어진 트리에서 아무 노드를 루트 노드로 정하고, 리프 노드부터 모두 0으로 만들어, 최종적으로
루트 노드를 0으로 만들면 된다.
리프 노드의 가중치가 -3이라고 하고, 그 부모 노드의 가중치는 2라고 하자.
리프 노드의 가중치를 0으로 만드려면 3을 더해야 하고, 부모 노드의 가중치는 3을 빼서 -1이 된다.
즉, 어떠한 노드가 하위 노드를 갖는다면, 하위노드의 가중치를 현재 노드의 가중치에 더하는 과정을
리프 노드부터 루트 노드까지 반복한다.
이때 더해지는 가중치의 값의 절대값들을 모두 더한 게 모든 노드를 0으로 만들기 위한 최소한의 행동 횟수이다.
모든 가중치를 0으로 만들 수 있는지는 루프 노드의 가중치가 0인지만 확인하면 되기 때문에, 굳이 하위 노드들의 실제 가중치를 0으로 만들어줄 필요는 없다.
코드
#include <string>
#include <vector>
#include <cmath>
using namespace std;
bool visited[300000];
long long answer=0;
void dfs(vector<long long> &vt, vector<vector<int>> &graph,int parent){
visited[parent]=true;
for(int i=0; i<graph[parent].size();i++){
if(visited[graph[parent][i]])
continue;
dfs(vt,graph,graph[parent][i]);
answer+=abs(vt[graph[parent][i]]);
vt[parent]+=vt[graph[parent][i]];
}
}
long long solution(vector<int> a, vector<vector<int>> edges) {
vector<long long> vt(a.begin(),a.end()); //a를 long long형으로 vt에 복사
vector<vector<int>> graph(a.size()); //주어진 간선으로 양방향 그래프 만들기
for(int i=0; i<edges.size();i++){
graph[edges[i][0]].push_back(edges[i][1]);
graph[edges[i][1]].push_back(edges[i][0]);
}
dfs(vt,graph,0);
if(vt[0]!=0)
return -1;
return answer;
}'알고리즘 문제 풀이 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 괄호 회전하기 kotlin (스택) 2022-06-24 코드 추가 (0) | 2021.07.04 |
|---|---|
| 프로그래머스 최댓값과 최솟값 kotlin (파싱) (0) | 2021.07.03 |
| 프로그래머스 실패율 c++ (해시,정렬) (0) | 2021.06.23 |
| 프로그래머스 멀쩡한 사각형 c++ (유클리드 호제) (0) | 2021.06.22 |
| 프로그래머스 짝지어 제거하기 c++(스택) (0) | 2021.06.21 |




댓글